Geometry Calculator - Calculate Area, Perimeter, Volume & Surface Area
Table of Contents
What is a Geometry Calculator?
A geometry calculator is a mathematical tool that computes measurements for two-dimensional (2D) and three-dimensional (3D) geometric shapes. This calculator uses standard geometric formulas to instantly determine area, perimeter, circumference, volume, and surface area based on the dimensions you provide. Whether you're a student working on homework, an engineer designing structures, or someone planning a home improvement project, a geometry calculator eliminates calculation errors and saves valuable time.
Geometry is a branch of mathematics that studies shapes, sizes, positions, and properties of space. The geometry calculator applies these mathematical principles to solve practical problems involving circles, triangles, rectangles, squares, trapezoids, spheres, cylinders, cones, cubes, and rectangular prisms. Each shape has specific formulas that relate its dimensions to measurable properties like area and volume. The calculator automates these calculations, providing accurate results in seconds.
Modern geometry calculators serve students from elementary school through university level, professionals in fields like architecture and construction, and anyone needing precise geometric measurements. The tool provides not just answers but also displays the formulas used, helping users understand the mathematical process. This educational approach makes geometry calculators valuable for both learning and practical application, bridging the gap between theoretical mathematics and real-world problem-solving.
Geometry Calculator
Calculate Geometric Properties
Select a shape and enter dimensions
Essential Geometry Formulas
Understanding geometric formulas is fundamental to solving spatial problems and calculating measurements accurately. These formulas represent mathematical relationships between different properties of shapes, allowing you to determine unknown measurements from known dimensions. Below are the essential formulas organized by shape type.
2D Shape Formulas
Two-dimensional shapes exist on a flat plane and have two dimensions: length and width. They have area (space inside) and perimeter (distance around the edge) but no volume.
Rectangle Formulas
For a rectangle with length (l) and width (w):
Perimeter = 2l + 2w = 2(l + w)
Diagonal = √(l² + w²)
Example: A rectangle with length 8 cm and width 5 cm has an area of 8 × 5 = 40 cm² and a perimeter of 2(8 + 5) = 26 cm.
Square Formulas
For a square with side length (s):
Perimeter = 4s
Diagonal = s√2
Example: A square with side length 6 cm has an area of 6² = 36 cm² and a perimeter of 4 × 6 = 24 cm.
Circle Formulas
For a circle with radius (r) and diameter (d = 2r):
Circumference = 2πr = πd
where π ≈ 3.14159
Example: A circle with radius 4 cm has an area of π × 4² ≈ 50.27 cm² and a circumference of 2π × 4 ≈ 25.13 cm.
Triangle Formulas
For a triangle with base (b), height (h), and sides (a, b, c):
Perimeter = a + b + c
Heron's Formula: Area = √[s(s-a)(s-b)(s-c)] where s = (a + b + c) ÷ 2
Example: A triangle with base 10 cm and height 6 cm has an area of ½ × 10 × 6 = 30 cm².
3D Shape Formulas
Three-dimensional shapes occupy space and have volume (amount of space inside) and surface area (total area of all outer surfaces).
Cube Formulas
For a cube with side length (s):
Surface Area = 6s²
Space Diagonal = s√3
Example: A cube with side length 4 cm has a volume of 4³ = 64 cm³ and surface area of 6 × 4² = 96 cm².
Rectangular Prism (Box) Formulas
For a rectangular prism with length (l), width (w), and height (h):
Surface Area = 2(lw + lh + wh)
Example: A box with dimensions 5 cm × 3 cm × 4 cm has a volume of 5 × 3 × 4 = 60 cm³.
Sphere Formulas
For a sphere with radius (r):
Surface Area = 4πr²
Example: A sphere with radius 3 cm has a volume of (4/3)π × 3³ ≈ 113.10 cm³ and surface area of 4π × 3² ≈ 113.10 cm².
Cylinder Formulas
For a cylinder with radius (r) and height (h):
Surface Area = 2πr² + 2πrh = 2πr(r + h)
Lateral Surface Area = 2πrh
Example: A cylinder with radius 3 cm and height 10 cm has a volume of π × 3² × 10 ≈ 282.74 cm³.
Cone Formulas
For a cone with radius (r), height (h), and slant height (l):
Surface Area = πr² + πrl = πr(r + l)
Slant Height: l = √(r² + h²)
Example: A cone with radius 4 cm and height 9 cm has a volume of (1/3)π × 4² × 9 ≈ 150.80 cm³.
Quick Reference Table
| Shape | Area/Volume Formula | Perimeter/Surface Area |
|---|---|---|
| Rectangle | A = l × w | P = 2(l + w) |
| Square | A = s² | P = 4s |
| Circle | A = πr² | C = 2πr |
| Triangle | A = ½bh | P = a + b + c |
| Cube | V = s³ | SA = 6s² |
| Sphere | V = (4/3)πr³ | SA = 4πr² |
| Cylinder | V = πr²h | SA = 2πr(r + h) |
| Cone | V = (1/3)πr²h | SA = πr(r + l) |
How This Calculator Works
Calculation Methodology
This geometry calculator implements mathematically verified formulas from established geometry principles. The calculation process follows a systematic approach that ensures accuracy and provides educational value through transparent formula display.
Step 1: Shape Selection and Recognition - When you select a shape, the calculator identifies which geometric formulas are applicable. Each shape has unique properties: 2D shapes require area and perimeter calculations, while 3D shapes need volume and surface area computations. The system loads the appropriate mathematical models for your selected shape.
Step 2: Input Validation and Processing - All dimensional inputs are validated to ensure they are positive numbers (negative dimensions are physically impossible). The calculator checks that required measurements are provided and converts all values to a consistent numerical format for processing. This prevents calculation errors from invalid or missing data.
Step 3: Formula Application - The calculator applies standard geometric formulas based on your shape selection. For circles, it uses π = 3.14159265359 for maximum precision. For triangles, it selects the appropriate formula based on available measurements (base-height for direct calculation, Heron's formula when all three sides are known). Each calculation follows the order of operations (PEMDAS/BODMAS) to ensure mathematical accuracy.
Step 4: Result Computation and Rounding - Calculations are performed using high-precision arithmetic, then rounded to two decimal places for practical use. The calculator maintains full precision during computation and only rounds the final display values, preventing cumulative rounding errors that occur when intermediate results are rounded.
Step 5: Unit Handling - Results are displayed with appropriate unit annotations. Area measurements receive square units (cm², m², ft²), volume measurements receive cubic units (cm³, m³, ft³), and linear measurements (perimeter, circumference) receive base units (cm, m, ft). This automatic unit handling prevents confusion about measurement types.
Step 6: Formula Documentation - Along with numerical results, the calculator displays the exact formula used, with your specific values substituted in. This transparency allows users to verify calculations manually, understand the mathematical process, and learn the underlying formulas for future reference.
Uses of a Geometry Calculator
A geometry calculator serves diverse purposes across education, professional work, and everyday life. Understanding its applications helps you leverage this tool effectively for various scenarios requiring spatial calculations.
Academic Learning and Homework
Students use geometry calculators to verify homework solutions, understand step-by-step calculation processes, and build confidence in mathematical problem-solving. The calculator serves as a learning aid by displaying formulas alongside results, helping students memorize geometric relationships. Teachers recommend using calculators to check work after attempting problems manually, ensuring understanding before moving to the next concept. This approach develops both computational skills and conceptual understanding of geometric principles.
Construction and Architecture
Construction professionals calculate material requirements using geometry. Determining floor area helps estimate flooring materials, calculating wall area guides paint purchases, and computing volumes indicates concrete needs for foundations. Architects use geometric calculations for space planning, ensuring rooms meet building codes and functional requirements. Accurate measurements prevent material waste and cost overruns, making geometry calculators essential planning tools.
Home Improvement and DIY Projects
Homeowners planning renovations need geometric calculations for countless projects. Installing new flooring requires accurate area calculations, building a deck needs precise perimeter and area measurements, and landscaping projects depend on volume calculations for mulch or soil. A geometry calculator ensures you purchase the right amount of materials, avoiding both shortages that delay projects and excess that wastes money.
Engineering and Manufacturing
Engineers design components with specific geometric properties. Mechanical engineers calculate volumes for fluid containers, civil engineers determine surface areas for coating applications, and manufacturing engineers compute material requirements for production. Geometric calculations affect product performance, material costs, and manufacturing feasibility. Precision matters significantly, making reliable calculation tools essential.
Art and Design
Artists and designers work with geometric shapes in their creations. Graphic designers calculate proportions for layouts, sculptors determine dimensions for three-dimensional works, and interior designers compute space requirements for furniture placement. Understanding geometric relationships helps create visually balanced, proportionally correct designs. The calculator speeds up the planning process while maintaining mathematical accuracy.
Packaging and Shipping
Businesses calculate packaging requirements using geometry. Determining box volumes helps estimate shipping costs, calculating surface areas guides packaging material purchases, and understanding dimensions ensures products fit in standard containers. E-commerce companies particularly rely on accurate geometric calculations for shipping cost estimation and packaging design, directly impacting profitability.
Science and Research
Scientists calculate geometric properties in experimental setups. Biologists determine cell volumes under microscopes, physicists calculate surface-to-volume ratios affecting heat transfer, and chemists compute reaction vessel capacities. Geometric calculations appear throughout scientific research, from molecular modeling to astronomical calculations. Accurate measurements ensure valid experimental results and reproducible research.
How to Use the Geometry Calculator
Follow this comprehensive guide to accurately calculate geometric properties for any shape using the calculator tool.
Step 1: Identify Your Shape
Determine which geometric shape matches your object or problem. Common 2D shapes include circles (perfectly round), rectangles (four sides with right angles, opposite sides equal), squares (four equal sides with right angles), and triangles (three-sided polygons). Common 3D shapes include spheres (perfectly round balls), cubes (six equal square faces), cylinders (circular ends with straight sides), and cones (circular base tapering to a point).
If your object doesn't perfectly match a geometric shape, approximate with the closest shape. For example, a tree trunk approximates a cylinder, a ball approximates a sphere, and a room floor approximates a rectangle.
Step 2: Select the Shape
Click the button corresponding to your shape in the shape selector grid. The button will highlight in purple, indicating it's active. The calculator will immediately update to show the relevant input fields for that shape. Each shape requires different measurements based on its geometric properties.
Step 3: Measure Your Dimensions
Use appropriate measuring tools to obtain accurate dimensions:
- For 2D shapes: Use a ruler, measuring tape, or digital measuring tool to measure lengths in centimeters, meters, inches, or feet
- For circles: Measure the radius (center to edge) or diameter (straight line through center). If you measure diameter, divide by 2 to get radius
- For 3D shapes: Measure height, width, depth, and radius as required. Ensure measurements are perpendicular and accurate
- For triangles: Measure the base (bottom side) and perpendicular height (vertical distance from base to opposite vertex)
Record all measurements with their units. Ensure all measurements for a single object use the same units.
Step 4: Enter Measurements
Type your measured values into the labeled input fields. Each field indicates what measurement it requires (length, width, radius, height, etc.). Enter only numerical values without units—the calculator will add appropriate units to results automatically. For example, if you measured a rectangle as 12.5 cm by 8 cm, enter "12.5" in the length field and "8" in the width field.
Step 5: Calculate Results
Click the "Calculate" button to perform the geometric calculations. The calculator will:
- Validate your inputs to ensure they're positive numbers
- Apply the appropriate geometric formulas
- Display all relevant measurements (area, perimeter, volume, surface area as applicable)
- Show the formulas used with your values substituted in
- Present results rounded to two decimal places with correct units
Step 6: Interpret Your Results
Understanding your results:
- Area (square units like cm², m², ft²) tells you the surface space covered by a 2D shape
- Perimeter/Circumference (linear units like cm, m, ft) tells you the distance around the edge
- Volume (cubic units like cm³, m³, ft³) tells you the space inside a 3D shape
- Surface Area (square units) tells you the total outer surface area of a 3D shape
Use these results for your specific application—ordering materials, solving homework problems, or planning projects.
Step 7: Try Different Shapes or Reset
To calculate properties for a different shape, simply click another shape button. Your previous results will clear automatically. To recalculate the same shape with different dimensions, click "Reset Calculator" to clear all fields and start fresh.
Frequently Asked Questions
Official References and Sources
Authoritative Geometry Resources
This geometry calculator is built upon established mathematical principles. The following official educational and mathematical resources provide authoritative information on geometric formulas and calculations:
- Khan Academy - High School Geometry - Comprehensive geometry lessons covering transformations, congruence, similarity, trigonometry, and analytic geometry aligned with Common Core standards.
- Education.com - Geometry Resources - Over 1,300 printable and digital resources covering fundamental geometric concepts including points, lines, angles, polygons, perimeters, areas, volumes, and surface areas.
- Calculator Soup - Geometry Calculators - Collection of geometry calculators covering formulas for standard 2D plane and 3D solid geometric shapes.
- BYJU'S - Geometry Formulas - Comprehensive list of basic and advanced geometry formulas for various shapes including curved surface areas, total surface areas, and volumes.
- Alloprof - Formulas for Perimeter, Area and Volume - Educational resource providing formulas for plane figures and three-dimensional solids used in secondary education.
3D shapes in primary school are taught as early as Year 1 when children encounter cuboids, pyramids and cones. Here is how to support children in KS1 and KS2 to understand what 3D shapes are, how to identify and recognise specific 3D shapes, and how we compare and contrast 3D shapes using a list of properties.
What are 3D shapes?
3D shapes are shapes with three dimensions, such as width, height and depth. An example of a 3D shape is a prism or a sphere. 3D shapes are multidimensional and can be physically held.
What does 3D mean
3D in 3D shapes stands for 3-dimensional. We normally talk about dimensions as measurements in a direction. Examples of dimensions include length, width or breadth, depth and height.
3D shapes example
Examples of 3D shapes are around us all the time. Nearly everything we see and interact with in our day to day lives is a three-dimensional shape, from Lego bricks to sunflowers. However, in the primary curriculum, children only need to know the names and understand the properties of the most common 3D shapes. This contrasts with 2D shapes where children must learn about both regular and irregular shapes.
Which 3D shapes will children learn?
In primary school, your child will learn about the following key geometric shapes: spheres, cones, prisms and pyramids. It’s worth knowing that geometrically prisms incorporate more solid shapes than you might traditionally think of as prisms. For example did you know that both a cube and a cuboid with a square base and straight sides are actually considered prisms.
What are the properties of 3D shapes?
The properties of 3D shapes are their faces, edges and vertices which all have specific meanings in the context of primary school maths lessons.
What is a face?
A face is a flat surface to a 3D object. For example a square based prism has 5 faces. A sphere has 1 curved surface but no face.
What is an edge?
An edge is where two line segments or faces meet. A cylinder has 2 edges.
What are vertices?
Vertices are where two lines or edges meet; in maths we refer to the corners of 3D shapes as vertices. The singular of vertices is actually vertex which can be a bit confusing. A cone has one vertex, and a cube has 4 vertices.
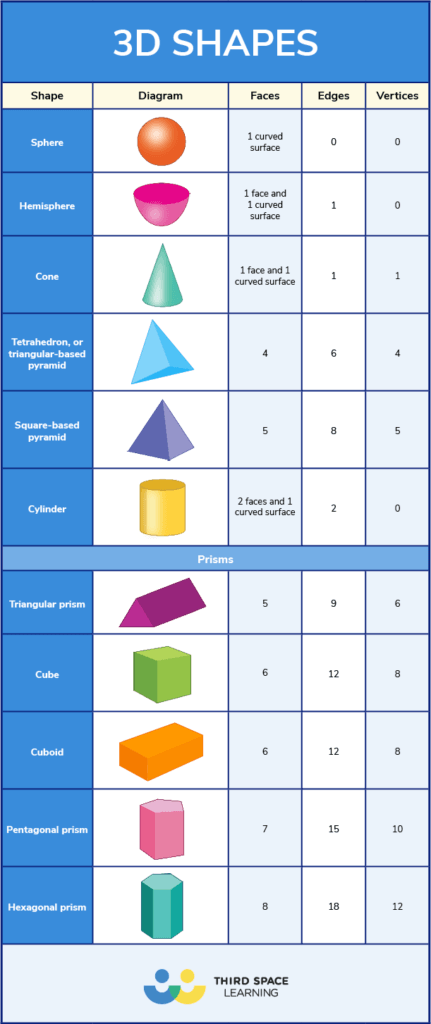
3D shapes names
These are the 3D shapes names:
- Sphere
- Hemisphere
- Cone
- Tetrahedron or Triangular-based pyramid
- Cylinder
- Triangular prism
- Hexagonal prism
- Pentagonal prism
- Cube
- Cuboid
Properties of 3D shapes
As well as the names, children need to know the properties of 3D shapes as listed below and in the printable table.
- A sphere has 1 curved surface.
- A hemisphere has 1 face, 1 curved surface and 1 edge.
- A cone has 1 face, 1 curved surface, 1 edge and 1 vertex.
- A tetrahedron, or triangular-based pyramid, has 4 faces, 6 edges and 4 vertices.
- A square-based pyramid has 5 faces, 8 edges and 5 vertices.
- A cylinder has 2 faces, 1 curved surface and 2 edges.
Prisms
- A triangular prism has 5 faces, 9 edges and 6 vertices.
- A cube has 6 faces, 12 edges and 8 vertices.
- A cuboid has 6 faces, 12 edges and 8 vertices.
- A pentagonal prism has 7 faces, 15 edges and 10 vertices.
- A hexagonal prism has 8 faces, 18 edges and 12 vertices.
When will my child learn about 3D shapes in primary school?
Geometry is taught in every year group in KS1 and KS2. Here’s what the National Curriculum expects to be taught about 2D shapes and 3D shapes, separated by year:
3D shapes in Year 1
Year 1 pupils should be able to:
- Recognise and name common 2-D and 3-D shapes, including: 2-D shapes [for example, rectangles (including squares), circles and triangles]; 3-D shapes [for example, cuboids (including cubes), pyramids and spheres].
- Non-statutory guidance: Pupils handle common 2-D and 3-D shapes, naming these and related everyday objects fluently. They recognise these shapes in different orientations and sizes, and know that rectangles, triangles, cuboids and pyramids are not always similar to each other.
3D shapes in Year 2
Year 2 pupils should be able to:
- Identify and describe the properties of 2-D shapes, including the number of sides and line of symmetry in a vertical line.
- Identify and describe the properties of 3-D shapes, including the number of edges, vertices and faces.
- Identify 2-D shapes on the surface of 3-D shapes, [for example, a circle on a cylinder and a triangle on a pyramid].
- Compare and sort common 2-D and 3-D shapes and everyday objects.
- Non-statutory guidance: Pupils handle and name a wide variety of common 2-D and 3-D shapes, including quadrilaterals and polygons, and cuboids, prisms and cones, and identify the properties of each shape (for example, number of sides, number of faces). Pupils identify, compare and sort shapes on the basis of their properties and use vocabulary precisely, such as sides, edges, vertices and faces.
3D shapes in Year 3
Year 3 pupils should be able to:
- Draw 2-D shapes and make 3-D shapes using modelling materials and recognise 3-D shapes in different orientations and describe them.
- Non-statutory guidance: Pupils’ knowledge of the properties of shapes is extended at this stage to symmetrical and non-symmetrical polygons and polyhedra. Pupils extend their use of the properties of shapes. They should be able to describe the properties of 2-D and 3-D shapes using accurate language, including lengths of lines and acute and obtuse for angles greater or lesser than a right angle.
3D shapes in Year 4
Year 4 pupils should be able to:
- Identify lines of symmetry in 2-D shapes presented in different orientations.
- Non-statutory guidance: Pupils continue to classify shapes using geometrical properties, extending to classifying different triangles (for example, isosceles, equilateral, scalene) and quadrilaterals (for example, parallelogram, rhombus, trapezium).
3D shapes in Year 5
Year 5 pupils should be able to:
- Identify 3-D shapes, including cubes and other cuboids, from 2-D representations and distinguish between regular and irregular polygons based on reasoning about equal sides and angles.
Year 6 pupils should be able to:
- Draw 2-D shapes using given dimensions and angles and recognise, describe and build simple 3-D shapes, including making nets.
How do 3D shapes relate to other areas of maths?
When working with fractions, children will often have to shade a fraction of a shape. They will have to relate their understanding of perimeter, area and volume to 3D shapes.
3D shapes questions
1. How many vertices on a cube?
(Answer: 8)
2. How many squares make up the net of a cube?
(Answer: 6)
3. Complete the table.
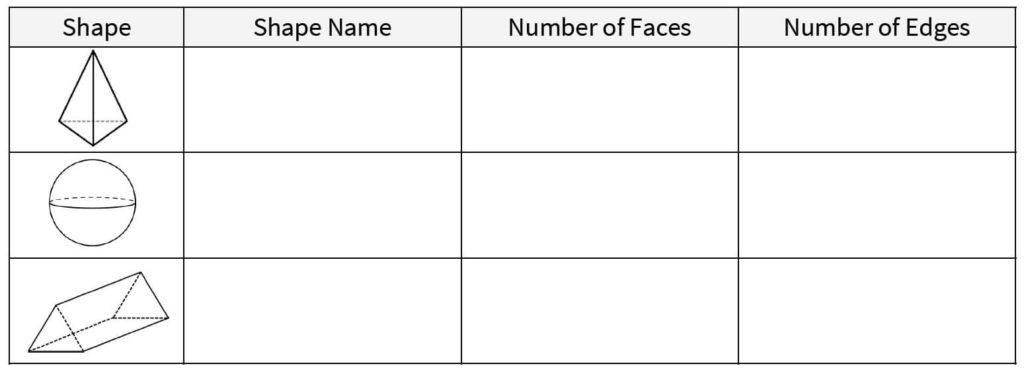
(Answer: Triangular based pyramid, 4 faces, 6 edges / Sphere, 0 faces, 0 edges / Triangular prism, 5 faces, 9 edges)
3D shapes worksheets
| 3-D Shapes: | ||
|
50 Frequently Asked Questions (FAQs) about “What Are 3D Shapes and Which 3D Shapes Names Do Kids Learn at Primary School”, each accompanied by detailed answers. These questions are curated based on trending searches and common inquiries related to 3D shapes in primary education.
1. What are 3D shapes?
3D shapes, or three-dimensional shapes, are geometric figures that have three dimensions: length, width, and height. Unlike 2D shapes, which have only length and width, 3D shapes occupy space and have volume. Common examples include cubes, spheres, cylinders, cones, and pyramids. They are fundamental in various fields such as mathematics, art, engineering, and everyday life.
2. Why are 3D shapes important in primary education?
Teaching 3D shapes in primary education is crucial because it helps children develop spatial awareness, problem-solving skills, and an understanding of the physical world. Recognizing and naming 3D shapes lays the foundation for more advanced mathematical concepts, geometry, and real-world applications. It also enhances cognitive development by encouraging visualization and critical thinking.
3. What are the basic 3D shapes taught in primary school?
In primary school, children typically learn the following basic 3D shapes:
- Cube
- Sphere
- Cylinder
- Cone
- Pyramid
- Rectangular Prism
- Triangular Prism
- Tetrahedron
These shapes are introduced through hands-on activities, visual aids, and interactive lessons to ensure comprehensive understanding.
4. What is a cube?
A cube is a 3D shape with six equal square faces, twelve equal edges, and eight vertices (corners). All angles in a cube are right angles (90 degrees). It’s a type of rectangular prism where all sides are of equal length. Common examples include dice, Rubik’s cubes, and some building blocks.
5. Can you describe a sphere?
A sphere is a perfectly round 3D shape where every point on its surface is equidistant from its center. It has no edges or vertices. Common examples of spheres include balls, globes, and bubbles. Spheres are unique because their symmetry allows for uniform properties in all directions.
6. What is a cylinder?
A cylinder is a 3D shape with two parallel circular bases connected by a curved surface. It has no vertices and two edges where the circular bases meet the curved surface. Examples include cans, pipes, and cylindrical storage containers. Cylinders can be open or closed, depending on whether the bases are present.
7. How do you define a cone?
A cone is a 3D shape with a single circular base and a pointed top called the apex. It has one curved surface and one edge where the base meets the curved surface. Examples of cones include ice cream cones, traffic cones, and party hats. Cones are known for their tapering shape from the base to the apex.
8. What is a pyramid?
A pyramid is a 3D shape with a polygonal base and triangular faces that converge at a single point called the apex. The most common pyramid is the square pyramid, which has a square base and four triangular faces. Examples include the pyramids of Egypt and certain types of tents. Pyramids are distinguished by their flat base and pointed top.
9. Describe a rectangular prism.
A rectangular prism is a 3D shape with six rectangular faces, twelve edges, and eight vertices. Unlike a cube, the lengths of its sides can vary, resulting in different dimensions. Common examples include boxes, bricks, and some types of buildings. Rectangular prisms are fundamental in understanding volume and surface area.
10. What is a triangular prism?
A triangular prism is a 3D shape with two identical triangular bases connected by three rectangular faces. It has five faces, nine edges, and six vertices. Examples include Toblerone chocolate bars and certain architectural structures. Triangular prisms are notable for their dual triangular ends and rectangular sides.
11. Can you explain what a tetrahedron is?
A tetrahedron is a 3D shape with four triangular faces, six edges, and four vertices. It is the simplest type of pyramid with a triangular base. Each face of a tetrahedron is an equilateral triangle, making it a regular polyhedron. Tetrahedrons are commonly seen in molecular structures and dice used in board games.
12. How do 3D shapes differ from 2D shapes?
3D shapes differ from 2D shapes in that they have three dimensions: length, width, and height, giving them volume and the ability to occupy space. 2D shapes only have two dimensions: length and width, and they lie flat on a plane without volume. For example, a cube (3D) versus a square (2D).
13. What are the characteristics of a cube?
A cube has the following characteristics:
- Faces: 6 equal square faces
- Edges: 12 equal edges
- Vertices: 8 vertices (corners)
- Angles: All angles are right angles (90 degrees)
- Symmetry: Highly symmetrical with equal dimensions on all sides
14. What real-life objects are shaped like spheres?
Real-life objects shaped like spheres include:
- Sports Balls: Basketballs, soccer balls, and tennis balls
- Bubbles: Soap bubbles
- Planets and Stars: Represented as spheres in models
- Ornaments: Decorative glass spheres
- Marbles: Small spherical glass or clay balls used in games
15. How can children recognize a cylinder in everyday life?
Children can recognize a cylinder by identifying objects with two circular bases and a curved surface. Examples include:
- Cans: Soda cans and food cans
- Pipes: Plumbing pipes
- Tubes: Paper towel tubes and mailing tubes
- Rolls: Toilet paper rolls and paper towel rolls
- Drums: Musical drums
16. What makes a cone unique among 3D shapes?
A cone is unique among 3D shapes because it has only one circular base and a single apex (point). Unlike other shapes that have multiple faces or edges, a cone tapers smoothly from its base to its apex, giving it a distinctive pointed top.
17. Can you name some pyramids other than the Egyptian pyramids?
Certainly! Besides the famous Egyptian pyramids, other pyramids include:
- Giza Pyramids: Specific pyramids in Egypt, such as the Great Pyramid of Giza
- Mesoamerican Pyramids: Like the Pyramid of the Sun in Teotihuacan, Mexico
- Ziggurats: Ancient Mesopotamian step pyramids, such as the Great Ziggurat of Ur
- Modern Pyramids: Structures like the Louvre Pyramid in Paris and the Luxor Hotel in Las Vegas
18. What are the uses of rectangular prisms in daily life?
Rectangular prisms are widely used in daily life for:
- Packaging: Boxes for shipping and storing goods
- Furniture: Bookshelves, cabinets, and refrigerators
- Building Construction: Bricks, concrete blocks, and building materials
- Household Items: Books, bricks, and storage containers
- Electronics: Televisions, computers, and appliances
19. How do triangular prisms appear in nature or man-made structures?
Triangular prisms appear in:
- Architecture: Certain roof designs and bridges
- Transportation: Trains and aircraft fuselages
- Games: Toblerone chocolate bars shaped like triangular prisms
- Crystals: Some crystal structures form triangular prisms
- Tents: Pyramid-shaped tents resembling triangular prisms
20. What makes a tetrahedron a regular polyhedron?
A tetrahedron is considered a regular polyhedron because all its faces are congruent equilateral triangles, and all its edges and angles are equal. This uniformity gives the tetrahedron a high degree of symmetry, making it the simplest of all regular polyhedrons.
21. How do primary school teachers introduce 3D shapes to kids?
Primary school teachers introduce 3D shapes through:
- Hands-On Activities: Using physical models and manipulatives
- Visual Aids: Flashcards, diagrams, and multimedia presentations
- Interactive Games: Shape matching games and building with blocks
- Real-Life Examples: Pointing out shapes in the classroom and around the community
- Art Projects: Creating 3D shapes using clay, paper, or other materials
- Storytelling: Incorporating shapes into stories and narratives
22. What educational tools help children learn 3D shapes?
Educational tools that help children learn 3D shapes include:
- Shape Blocks: Building blocks in various 3D shapes
- Manipulatives: Geometric solids and tactile models
- Educational Software: Interactive apps and online games
- Flashcards: Visual cards with names and images of shapes
- Workbooks: Worksheets and coloring books focused on 3D shapes
- Puzzles: 3D shape puzzles and matching games
23. How can parents reinforce the learning of 3D shapes at home?
Parents can reinforce 3D shape learning at home by:
- Identifying Shapes: Pointing out 3D shapes in everyday objects
- Building Models: Using blocks, LEGO, or other building toys to create shapes
- Art Projects: Crafting 3D shapes with paper, clay, or recycled materials
- Educational Games: Playing shape recognition games and quizzes
- Reading Books: Sharing children’s books that focus on shapes
- Interactive Activities: Using household items for sorting and categorizing shapes
24. What are the benefits of learning 3D shapes in primary school?
Benefits of learning 3D shapes in primary school include:
- Spatial Awareness: Enhances the ability to visualize and manipulate objects in space
- Mathematical Foundation: Builds a basis for geometry and more advanced math concepts
- Problem-Solving Skills: Encourages critical thinking and analytical skills
- Creativity: Stimulates creative expression through building and crafting
- Real-World Application: Connects mathematical concepts to everyday life
- Cognitive Development: Promotes memory, attention to detail, and logical reasoning
25. What challenges might children face when learning 3D shapes?
Children might face challenges such as:
- Spatial Visualization: Difficulty in visualizing and understanding 3D structures
- Naming and Differentiating: Confusion between similar shapes, like cubes and rectangular prisms
- Understanding Properties: Grasping the properties like faces, edges, and vertices
- Application: Applying shape knowledge to real-world contexts
- Engagement: Maintaining interest and motivation in learning abstract concepts
- Language Barrier: Struggling with the terminology associated with 3D shapes
26. How can technology be used to teach 3D shapes effectively?
Technology can enhance 3D shape learning through:
- Interactive Apps: Educational apps that allow virtual manipulation of shapes
- Virtual Reality (VR): Immersive environments where students can explore 3D shapes
- Online Games: Engaging games that reinforce shape recognition and properties
- Educational Videos: Visual explanations and demonstrations of 3D concepts
- 3D Modeling Software: Tools for creating and experimenting with digital 3D models
- Augmented Reality (AR): Overlaying digital shapes onto the real world for interactive learning
27. What role do manipulatives play in learning 3D shapes?
Manipulatives play a crucial role by providing hands-on experiences that help children:
- Visualize Shapes: Physical models make abstract concepts tangible
- Explore Properties: Children can touch and manipulate shapes to understand faces, edges, and vertices
- Build Spatial Skills: Constructing shapes enhances spatial reasoning and coordination
- Encourage Creativity: Allows for creative expression through building and designing
- Facilitate Engagement: Interactive learning tools increase interest and participation
28. What is the difference between a cube and a rectangular prism?
The primary differences between a cube and a rectangular prism are:
- Faces: A cube has six equal square faces, while a rectangular prism has six rectangular faces with varying lengths and widths
- Edges: All edges of a cube are equal, whereas a rectangular prism has edges of different lengths
- Symmetry: A cube is highly symmetrical with all sides identical, whereas a rectangular prism has less symmetry due to unequal sides
29. How do teachers assess students’ understanding of 3D shapes?
Teachers assess understanding of 3D shapes through:
- Quizzes and Tests: Multiple-choice, fill-in-the-blank, and drawing questions
- Hands-On Projects: Building models or creating 3D art projects
- Oral Presentations: Describing shapes and their properties verbally
- Interactive Games: Observing participation and accuracy in shape-based games
- Worksheets: Completing exercises that involve identifying and labeling shapes
- Peer Assessments: Collaborative activities where students evaluate each other’s work
30. What are some common misconceptions about 3D shapes?
Common misconceptions include:
- Confusing 2D and 3D Shapes: Difficulty distinguishing between flat and solid shapes
- Incorrect Naming: Misnaming shapes due to similar appearances
- Property Misunderstanding: Not accurately identifying the number of faces, edges, or vertices
- Shape Rotation: Struggling to recognize shapes when viewed from different angles
- Volume vs. Surface Area: Confusing concepts related to volume and surface area of shapes
31. How can art and creativity be integrated into learning 3D shapes?
Art and creativity can be integrated by:
- Craft Projects: Creating 3D shapes using paper, clay, or recycled materials
- Drawing and Coloring: Illustrating and coloring different 3D shapes
- Sculpture: Building sculptures that incorporate various 3D shapes
- Collage Making: Assembling collages using cut-out shapes
- Storytelling Art: Designing scenes or characters using 3D shapes
- Interactive Installations: Constructing interactive displays that demonstrate shape properties
32. What resources are available online for teaching 3D shapes?
Online resources for teaching 3D shapes include:
- Educational Websites: Sites like Khan Academy, ABCya, and Education.com offer lessons and activities
- YouTube Channels: Educational videos that explain and demonstrate 3D shapes
- Interactive Games: Online games that reinforce shape recognition and properties
- Printable Worksheets: Downloadable worksheets and coloring pages
- Virtual Manipulatives: Digital tools for exploring and building 3D shapes
- Lesson Plans: Comprehensive lesson plans available on platforms like Teachers Pay Teachers
33. How do 3D shapes relate to other areas of the curriculum?
3D shapes relate to various curriculum areas such as:
- Mathematics: Geometry, measurement, and spatial reasoning
- Science: Understanding molecular structures, physical properties, and engineering concepts
- Art: Sculpting, design, and creative expression using shapes
- Technology: 3D modeling and computer-aided design (CAD)
- Physical Education: Games and activities that involve spatial movement and coordination
- Language Arts: Descriptive writing and storytelling involving shapes
34. What are the key properties of a sphere?
Key properties of a sphere include:
- Surface: Completely smooth and round without any edges or vertices
- Symmetry: Perfectly symmetrical around its center
- Curvature: Uniform curvature at every point on the surface
- Volume: Represents maximum volume for a given surface area among all shapes
- Equidistance: All points on the surface are equidistant from the center
35. How can games be used to teach 3D shapes?
Games can make learning 3D shapes fun and engaging by:
- Shape Bingo: Using cards with different 3D shapes
- Memory Matching: Matching names with corresponding shape images
- Building Challenges: Using blocks or LEGO to construct specific shapes
- Online Quizzes: Interactive quizzes that test shape recognition and properties
- Puzzle Games: Solving 3D shape puzzles and jigsaw pieces
- Role-Playing Games: Acting out or building stories around different shapes
36. What are the properties of a cylinder?
Properties of a cylinder include:
- Faces: Two parallel circular bases and one curved surface
- Edges: Two circular edges where the bases meet the curved surface
- Vertices: No vertices
- Symmetry: Infinite lines of symmetry around the central axis
- Volume and Surface Area: Defined by the radius of the base and the height
37. Why is spatial awareness important for children?
Spatial awareness is crucial because it:
- Enhances Problem-Solving: Helps children navigate and solve spatial-related problems
- Supports Learning in STEM: Essential for subjects like math, science, engineering, and technology
- Improves Coordination: Aids in physical activities and fine motor skills
- Facilitates Everyday Tasks: Assists in tasks like reading maps, assembling objects, and organizing spaces
- Boosts Cognitive Development: Encourages critical thinking and memory skills
38. What activities can help children distinguish between different 3D shapes?
Activities include:
- Sorting Games: Sorting objects based on their shapes
- Building Projects: Constructing various 3D shapes using materials like clay or blocks
- Shape Hunts: Searching for and identifying shapes in the classroom or home
- Drawing and Labeling: Drawing 3D shapes and labeling their parts
- Interactive Software: Using educational apps that focus on shape differentiation
- Role-Playing: Acting out the properties of different shapes
39. How do 3D shapes appear in architecture?
3D shapes are fundamental in architecture by:
- Designing Structures: Using cubes, spheres, cylinders, and pyramids in building designs
- Creating Symmetry: Implementing symmetrical shapes for aesthetic and structural balance
- Enhancing Functionality: Incorporating shapes that serve specific purposes, like domes or arches
- Innovative Designs: Exploring unconventional shapes for modern and artistic buildings
- Structural Integrity: Using shapes that provide strength and stability to structures
40. What is the difference between a pyramid and a prism?
The differences include:
- Faces: A pyramid has a polygonal base and triangular faces that converge at an apex, while a prism has two identical polygonal bases connected by rectangular faces
- Edges: Pyramids have fewer edges compared to prisms with more edges due to additional rectangular sides
- Vertices: Pyramids have one apex, whereas prisms have two corresponding vertices on each base
- Symmetry: Pyramids taper to a point, whereas prisms maintain parallel and uniform sides
41. How can 3D shapes be used to teach measurement concepts?
3D shapes can be used to teach measurement by:
- Volume: Calculating the space inside a shape
- Surface Area: Measuring the total area of all faces
- Dimensions: Understanding length, width, and height
- Comparisons: Comparing sizes and dimensions of different shapes
- Real-World Applications: Measuring objects like boxes or containers in daily life
- Practical Exercises: Building and measuring models to apply mathematical concepts
42. What are some common tools used to create 3D shapes in the classroom?
Common tools include:
- Building Blocks: LEGO, wooden blocks, and magnetic blocks
- Clay or Play-Doh: For molding and shaping
- Paper and Cardboard: For constructing paper models
- Geometric Solids: Plastic or wooden models of various 3D shapes
- 3D Printers: For advanced classrooms to create precise models
- Craft Supplies: Scissors, glue, rulers, and markers for assembling shapes
43. How do 3D shapes relate to real-world engineering and design?
3D shapes are integral to engineering and design by:
- Structural Design: Using shapes like cubes, spheres, and cylinders for building frameworks
- Aerodynamics: Designing objects like cars and airplanes with streamlined shapes
- Product Design: Creating functional and aesthetically pleasing products using various shapes
- Architecture: Developing buildings and structures with specific shape properties for stability and aesthetics
- Mechanics: Understanding how different shapes interact in machinery and mechanical systems
44. What are the key properties of a pyramid?
Key properties of a pyramid include:
- Faces: A polygonal base and triangular faces that meet at the apex
- Edges: Defined by the base edges and the edges connecting the base to the apex
- Vertices: One apex and vertices corresponding to the base’s corners
- Volume and Surface Area: Calculated based on the base area and height
- Symmetry: Varies based on the base shape; regular pyramids have symmetrical triangular faces
45. How can storytelling be used to teach 3D shapes?
Storytelling can engage children by:
- Character Creation: Introducing characters shaped like different 3D shapes
- Adventure Narratives: Crafting stories where shapes solve problems or embark on journeys
- Interactive Stories: Encouraging children to identify and describe shapes within the story
- Visual Aids: Using illustrations and props to represent shapes in the narrative
- Role-Playing: Acting out parts of the story using 3D shape models
46. What are the properties of a tetrahedron?
Properties of a tetrahedron include:
- Faces: 4 triangular faces, all congruent in a regular tetrahedron
- Edges: 6 equal edges in a regular tetrahedron
- Vertices: 4 vertices where the edges meet
- Symmetry: Highly symmetrical with equal angles and sides
- Volume and Surface Area: Defined by the edge length and the number of faces
47. How can children use everyday objects to learn about 3D shapes?
Children can use everyday objects by:
- Identification: Naming shapes of common items like balls (spheres) and boxes (cubes)
- Classification: Sorting objects based on their shapes
- Counting: Counting faces, edges, and vertices of household items
- Building: Using objects to create new shapes or structures
- Comparison: Comparing different objects to understand shape variations
48. What are the educational standards for teaching 3D shapes in primary school?
Educational standards typically include:
- Recognition and Naming: Identifying and naming common 3D shapes
- Understanding Properties: Learning the number of faces, edges, and vertices
- Spatial Reasoning: Developing the ability to visualize and manipulate shapes in space
- Application: Applying shape knowledge to solve real-world problems
- Integration with Other Subjects: Linking geometry with art, science, and technology
- Assessment: Evaluating understanding through various assessment methods
Standards may vary by region but generally align with national or state educational guidelines for mathematics.
49. How can 3D shapes be used to enhance fine motor skills in children?
Building and manipulating 3D shapes can enhance fine motor skills by:
- Handling Objects: Grasping, moving, and positioning shapes improves hand-eye coordination
- Crafting: Cutting, gluing, and assembling shapes develop dexterity and precision
- Building Structures: Stacking and arranging shapes require control and coordination
- Manipulative Play: Engaging with small objects enhances finger strength and flexibility
- Art Projects: Creating detailed 3D models fosters meticulous hand movements
50. What are some advanced 3D shapes introduced in later primary grades?
In later primary grades, children may be introduced to more complex 3D shapes, including:
- Hexagonal Prism: A prism with hexagonal bases and rectangular faces
- Octahedron: A polyhedron with eight triangular faces
- Dodecahedron: A polyhedron with twelve pentagonal faces
- Icosahedron: A polyhedron with twenty triangular faces
- Ellipsoid: A shape resembling a stretched or compressed sphere
- Torusk: A doughnut-shaped object
These shapes help deepen students’ understanding of geometry and prepare them for more advanced mathematical concepts.



