What is Mastery of Mathematics?

Mastery of mathematics is not a fixed state but a continuum. At each stage of learning, pupils should acquire and demonstrate sufficient grasp of the mathematics relevant to their year group, so that their learning is sustainable over time and can be built upon in subsequent years.  

This requires development of depth through looking at concepts in detail using a variety of representations and contexts and committing key facts, such as number bonds and times tables, to memory. 

(Teaching for Mastery, NCETM 2015)

Our curriculum aims to embed the principles of a teaching for mastery approach underpinned with the belief that ‘every child can achieve in maths’.

Key Research

Research informed curriculum and pedagogical choices:

The Essence of Maths Teaching for Mastery NCETM

  • Mathematics Mastery
  • Jerome Bruner (1915 – 2016) Cognitive development research.
  • Richard Skemp (1919-1995) Relational Understanding and Instrumental Understanding. 1976
  • Zoltan Dienes (1916-2014) Systematic Variation
  • EEF: Mastery Learning + 5 months
    Mastery learning | EEF (educationendowmentfoundation.org.uk)
  • EEF Guidance Improving Mathematics (2020):

Improving Mathematics in the Early Years and Key Stage 1 | EEF (educationendowmentfoundation.org.uk)

Improving Mathematics in Key Stages 2 and 3 | EEF (educationendowmentfoundation.org.uk)

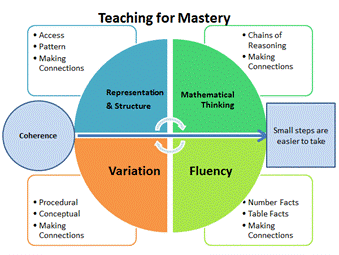
The 5 Big Ideas of Teaching for Mastery

Our curriculum and pedagogical choices are underpinned by the five big ideas of teaching for mastery:

(Taken from NCETM March 2017)

  • Coherence
    Lessons are broken down into small connected steps that gradually unfold the concept, providing access for all children and leading to a generalisation of the concept and the ability to apply the concept to a range of contexts.
  • Representation and Structure
    Representations used in lessons expose the mathematical structure being taught, the aim being that students can do the maths without recourse to the representation
  • Mathematical Thinking
    If taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned with and discussed with others
  • Fluency
    Quick and efficient recall of facts and procedures and the flexibility to move between different contexts and representations of mathematics
  • Variation
    Variation is twofold. It is firstly about how the teacher represents the concept being taught, often in more than one way, to draw attention to critical aspects, and to develop deep and holistic understanding. It is also about the sequencing of the episodes, activities and exercises used within a lesson and follow up practice, paying attention to what is kept the same and what changes, to connect the mathematics and draw attention to mathematical relationships and structure.

Mastery of Mathematics at Lansbury Lawrence

At Lansbury Lawrence, our maths curriculum has been designed to coherently sequence learning across EYFS to KS2. In response to the Pandemic, our curriculum was adapted and prioritised to meet the needs of all children in our school, which was supported through our partnerships with the NCETM, London North & South East Maths Hub and White Rose Maths.

Curriculum Aims:

Through our curriculum, we aim to develop mathematicians who:

  • have a strong number sense
  • can see patterns and make generalisations
  • are articulate in their books and out loud
  • make reasoned decisions and justify them
  • think critically about their own and other’s strategies
  • are equipped to solve unfamiliar problems in a range of contexts.

To achieve this our curriculum has:

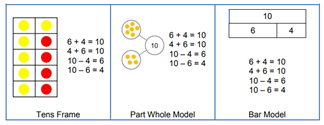
  • a consistent set of concrete and pictorial representations from EYFS to Year 6

(NCETM 2015)

  • ensures all children experience coherent and progressive models throughout the school to support deep and sustained learning.
  • ensures lessons plan opportunities for children to make connections. For example:
  • Additive reasoning
  • Multiplicative reasoning
  • Fractions with ratio
  • Links to prior learning
  • takes a problem-solving approach to modelled, guided, and independent work
  • provides daily opportunities for children to meaningfully rehearse their number facts to develop fluency and confidence:
  • Number Sense Maths Programme EYFS & KS1
  • Multiplication Table facts in LKS2
  • Arithmetic and Recapping KS2
  • ensures that explicitly explaining and justifying process is critical when working as a class, in a group or independently.
  • provides challenge and scaffolds so that all children move through the curriculum broadly at the same pace
  • focuses on conceptual understanding
  • Provides a framework of vocabulary, key terms and phrases.

For this to happen, our teachers are supported to:

  • understand the fundamentals of number
  • understand the progression from concrete to visual to abstract is not linear and each stage should be revisited as needed.
  • use modelled and shared sessions to promote choice, critical thinking and a diversity of ideas.
  • use a range of questioning that support all children to reflect on, explain and extend their thinking.
  • scaffold work so all children reach the same goals
  • explicitly model new learning using strategies such as the ‘silent teacher’ and worked example approach
  • anticipate and teach away from misconceptions
  • know potential sticking points in lessons and plan accordingly
  • be precise in their use of vocabulary and expectation of children’s vocabulary
  • know progression within each unit to assess, intervene and know when all children are ready to move on.

Our classrooms:

  • map the progression of models used throughout the year
  • have updated working walls that support the unit being taught
  • are fully equipped with a range of manipulatives accessible to all the children all of the time.

Response to the Pandemic:

We followed advice from the DfE Teaching Mathematics in Primary Schools guidance; Teaching mathematics in primary schools – GOV.UK (www.gov.uk) which offered support by:

  • identifying the core concepts that are needed for pupils to progress in their study of mathematics
  • demonstrating how pupils can build their understanding of these concepts from year 1 to year 6

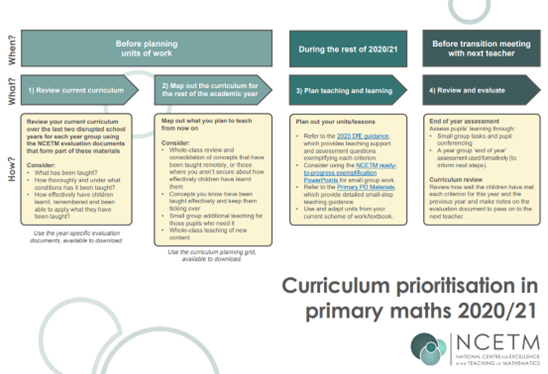
This supported our decisions on what to prioritise to ensure children developed firm foundations before moving on to new content. Our planning and review process is exemplified in the flow chart below:

One notable gap in children’s knowledge upon returning to school was number facts and quick mental recall of these to perform formal algorithms. To address this, we have timetabled 15-minute daily fluency sessions in all year groups:

These are regularly assessed and reviewed to support progress of all children.

NCETM Curriculum Prioritisation in Primary Maths:

From September 2021, our curriculum map was supported by the NCETM prioritisation framework which:

‘… provides coherent sequencing for the primary maths curriculum. It draws together the DfE guidance on curriculum prioritisation, with the high quality professional development and classroom resources provided by the NCETM Primary Mastery PD materials.’

We supplement this with White Rose Maths and online tools such as Learning by Questions.

cp-overview-years-1-6_08122021.pdf (ncetm.org.uk)