What is Gravitational Force?
According to Newton’s universal law of gravitation,
The force of attraction between any two bodies is directly proportional to the product of their masses and is inversely proportional to the square of the distance between them.
Gravitational Force Calculator
Results
-
Gravitational Formula Reference
F = G × (m₁ × m₂) / r²
Where:
- F = Gravitational force (N)
- G = Gravitational constant (6.674 × 10⁻¹¹ N·m²/kg²)
- m₁ = Mass of first object (kg)
- m₂ = Mass of second object (kg)
- r = Distance between the centers of the masses (m)
Newton’s cannonball is a ‘thought experiment’ given by Newton, which leads to the hypothesis that the force of gravity is universal, and it plays a major role in planetary motion.
According to this thought experiment, he assumed a cannon on the top of a very high mountain peak. The following cases can arise if the cannon is loaded with gunpowder and fired.
- If the speed of the cannon is low, it falls on the Earth following a projectile motion.
- If at that particular altitude, the speed of the cannon is equal to the orbital speed, the cannonball will go on circling the Earth about a fixed orbit.
- If the speed of the cannonball is higher than the orbital velocity but is insufficient to leave the Earth, i.e. less than the escape velocity of the Earth then, the cannonball continues to revolve around Earth in an elliptical orbit.
- If the speed is equal to escape velocity or greater than that, the cannonball leaves the Earth in a parabolic or hyperbolic trajectory.
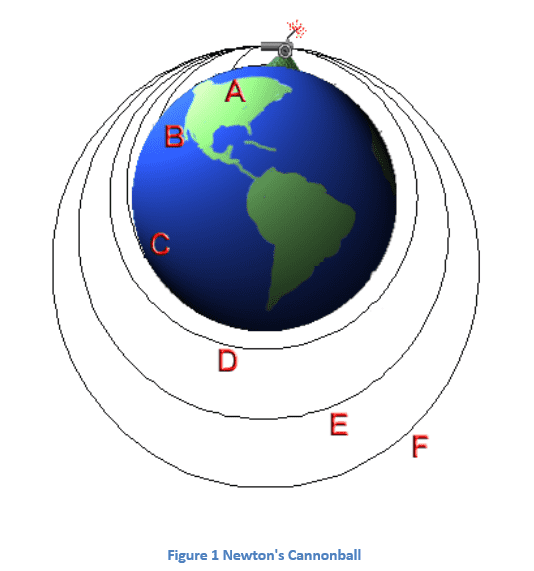
Table of Contents
- Introduction to Gravitational Force
- Newton’s Law of Universal Gravitation
- Historical Context and Conceptual Overview
- Detailed Breakdown of the Gravitational Force Formula
- Newton’s Cannonball Thought Experiment
- Planetary Motion and Gravity
- Practical Applications and Everyday Examples
- Solved Problems on Gravitational Force
- Frequently Asked Questions (FAQ)
- Summary and Conclusion
1. Introduction to Gravitational Force
Gravity is the fundamental force that influences the motion of objects both on Earth and in the cosmos. It is the force that:
- Keeps us anchored to the ground.
- Causes objects to accelerate toward Earth.
- Maintains the Moon’s orbit around our planet.
- Governs the elliptical orbits of planets around the Sun.
- Influences the trajectories of comets, asteroids, and even light near massive objects.
At its core, gravity is the attractive interaction between any two masses. Sir Isaac Newton was the first to mathematically formalize this phenomenon, establishing the principles of classical mechanics that still serve as a basis for modern physics.
2. Newton’s Law of Universal Gravitation
2.1. Mathematical Expression
Newton’s law of universal gravitation provides a precise mathematical description of how two masses interact. It states that every particle in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This relationship is expressed as:
\(\displaystyle F = G \frac{m_1 m_2}{r^2}\)
Where:
- \( F \) is the gravitational force between the two bodies (in Newtons, N).
- \( m_1 \) and \( m_2 \) are the masses of the two objects (in kilograms, kg).
- \( r \) is the distance between the centers of the two masses (in meters, m).
- \( G \) is the universal gravitational constant, approximately \( 6.67430 \times 10^{-11} \, \text{m}^3\, \text{kg}^{-1}\, \text{s}^{-2} \).
2.2. Understanding the Components
Gravitational Force \( F \): This represents the strength of the attraction between two objects. It is responsible for various phenomena, including the fall of objects on Earth and the orbital motion of satellites.
Masses \( m_1 \) and \( m_2 \): The product \( m_1 m_2 \) indicates that the gravitational force increases as the masses increase. For instance, the immense mass of the Sun creates a strong gravitational field that orchestrates the movement of the planets.
Distance \( r \): The term \( r^2 \) in the denominator demonstrates the inverse square law: the gravitational force decreases rapidly with increasing distance. Doubling the distance between two masses reduces the force to one-fourth of its original value.
Universal Gravitational Constant \( G \): This constant ensures that the gravitational force is calculated correctly across different systems. Although its value is very small, it standardizes the equation, making it applicable from everyday scenarios to cosmic phenomena.
3. Historical Context and Conceptual Overview
The concept of gravity has evolved through centuries of observation and experimentation. Before Newton’s groundbreaking work, many philosophers and scientists pondered the reasons behind falling objects and the motion of celestial bodies.
Key Historical Milestones:
- Newton’s Insight: Motivated by observations such as an apple falling from a tree, Newton proposed that the force causing objects to fall on Earth was the same force that governed the orbits of the Moon and planets.
- Unified Framework: Newton’s law unified terrestrial and celestial mechanics, demonstrating that a single force could explain a wide array of physical phenomena.
- Cavendish Experiment: While Newton established the theory, Henry Cavendish later measured \( G \) in 1798 using a torsion balance, providing the necessary precision to calculate gravitational forces accurately.
Newton’s insights laid the foundation for modern physics, influencing not only astronomy but also engineering and technology.
4. Detailed Breakdown of the Gravitational Force Formula
4.1. Direct Proportionality to Mass
The numerator of the equation, \( m_1 m_2 \), shows that the gravitational force is directly proportional to the masses of the objects. This means that a more massive body will exert a stronger gravitational pull on other objects. For example, while a small object like a book experiences gravity, the effect is much more pronounced for massive objects like planets and stars.
4.2. The Inverse Square Law
The \( r^2 \) term in the denominator embodies the inverse square law, which states that the gravitational force decreases rapidly as the distance increases. In mathematical terms, if the distance \( r \) between two objects is doubled, the gravitational force becomes:
\(\displaystyle F \propto \frac{1}{(2r)^2} = \frac{1}{4r^2}\)
This rapid decline in force is why distant stars, despite their massive sizes, exert only a minimal gravitational pull on us.
4.3. The Role of \( G \)
The universal gravitational constant \( G \) calibrates the equation so that it works universally. Its small value ensures that while gravity is the dominant force on large scales (such as in planetary orbits), it is relatively weak when dealing with small masses or short distances.
5. Newton’s Cannonball Thought Experiment
Newton’s cannonball thought experiment is a classic illustration that demonstrates how gravity can produce orbital motion.
The Experiment Explained
Imagine a cannon positioned atop an extremely tall mountain. When the cannon fires a cannonball horizontally:
- Low Speed: At low speeds, the cannonball follows a curved, parabolic trajectory and eventually falls to the ground.
- Orbital Speed: At a specific critical speed—known as orbital velocity—the cannonball falls toward Earth at the same rate that the Earth curves away, resulting in a continuous circular orbit.
- Higher Speed: If the cannonball is fired faster than the orbital velocity (but below escape velocity), it enters an elliptical orbit around the Earth.
- Escape Velocity: At speeds equal to or greater than the escape velocity, the cannonball overcomes Earth’s gravitational pull and escapes into space.
This thought experiment demonstrates that gravity is not merely a force that pulls objects downward; it is also responsible for the orbital motion of celestial bodies. The same force that causes an apple to fall also keeps the Moon in orbit around the Earth and the planets in orbit around the Sun.
6. Planetary Motion and Gravity
Gravity is the primary force that governs the motion of planets and other celestial bodies. Let’s see how gravity controls planetary motion.
6.1. Gravitational Force in Orbits
The gravitational force between the Sun and a planet is given by:
\(\displaystyle F = G \frac{M_{\text{Sun}}\, m_{\text{planet}}}{r^2}\)
Where:
- \( M_{\text{Sun}} \) is the mass of the Sun.
- \( m_{\text{planet}} \) is the mass of the planet.
- \( r \) is the distance between the Sun and the planet.
6.2. Balancing Gravity and Inertia
A planet remains in its orbit due to a balance between:
- Gravitational Attraction: The pull of the Sun draws the planet inward.
- Tangential Velocity (Inertia): The planet’s sideways motion prevents it from falling directly into the Sun.
This balance is similar to swinging a ball on a string; the ball’s inertia keeps it moving forward while the string’s tension (analogous to gravity) constantly pulls it inward.
6.3. The Moon-Earth System
The same principles apply to the Moon’s orbit around the Earth. The gravitational force is:
\(\displaystyle F = G \frac{M_{\text{Earth}}\, m_{\text{Moon}}}{r^2}\)
Where:
- \( M_{\text{Earth}} \) is the mass of the Earth.
- \( m_{\text{Moon}} \) is the mass of the Moon.
- \( r \) is the distance between the Earth and the Moon.
The Moon’s tangential velocity is just enough to maintain its orbit, preventing it from colliding with Earth.
7. Practical Applications and Everyday Examples
7.1. Everyday Experiences
- Falling Objects: Any object, whether it’s a pen or an apple, falls toward the Earth due to gravity.
-
Weight: Your weight is the gravitational force acting on your mass, expressed as:
\(\displaystyle F = m\, g\), where \( g \approx 9.8 \, \text{m/s}^2 \). - Walking and Standing: Gravity keeps us grounded, making everyday activities possible.
7.2. Astronomical Phenomena
- Planetary Orbits: The orbits of planets around the Sun are maintained by the gravitational force.
- Tidal Forces: The Moon’s gravitational pull generates tides on Earth.
- Galactic Dynamics: Gravity plays a crucial role in the formation and evolution of stars, galaxies, and clusters of galaxies.
- Black Holes: In extreme cases, such as black holes, gravity becomes so intense that even light cannot escape.
7.3. Engineering and Space Exploration
- Satellite Deployment: Calculations based on Newton’s law ensure that satellites maintain a stable orbit.
- Space Missions: Understanding gravity is essential for planning space missions, orbital insertions, and flybys.
- Tidal Energy: Some coastal regions harness the gravitational pull of the Moon to generate tidal energy.
8. Solved Problems on Gravitational Force
8.1. Problem 1: Force of Gravity at Earth’s Surface
Given:
- Mass of the object: \( m_2 = 1000 \, \text{kg} \)
- Mass of Earth: \( m_1 = 5.98 \times 10^{24} \, \text{kg} \)
- Radius of Earth: \( r = 6.38 \times 10^6 \, \text{m} \)
- Universal gravitational constant: \( G = 6.67 \times 10^{-11} \, \text{m}^3\, \text{kg}^{-1}\, \text{s}^{-2} \)
Step-by-Step Calculation:
-
Compute the square of the radius:
\(\displaystyle r^2 = \left(6.38 \times 10^6 \, \text{m}\right)^2 = 4.0704 \times 10^{13} \, \text{m}^2\) -
Calculate the product of the masses:
\(\displaystyle m_1 m_2 = \left(5.98 \times 10^{24} \, \text{kg}\right) \times \left(1000 \, \text{kg}\right) = 5.98 \times 10^{27} \, \text{kg}^2\) -
Apply the gravitational force formula:
\(\displaystyle F = G \frac{m_1 m_2}{r^2} = \left(6.67 \times 10^{-11}\right) \frac{5.98 \times 10^{27}}{4.0704 \times 10^{13}}\) -
Perform the calculation:
\(\displaystyle F \approx 9.778 \times 10^3 \, \text{N}\)
Answer: The gravitational force at the Earth’s surface is approximately \( 9778 \, \text{N} \), which agrees with the relation \( F = m\,g \) where \( g \approx 9.8 \, \text{m/s}^2 \).
8.2. Problem 2: Force of Gravity 10,000 Meters Above Earth
Given:
- Mass of the object: \( m_2 = 1000 \, \text{kg} \)
- Mass of Earth: \( m_1 = 5.98 \times 10^{24} \, \text{kg} \)
- Height above Earth: \( h = 10,000 \, \text{m} \)
- Radius of Earth: \( R = 6.38 \times 10^6 \, \text{m} \)
- Universal gravitational constant: \( G = 6.67 \times 10^{-11} \, \text{m}^3\, \text{kg}^{-1}\, \text{s}^{-2} \)
Step-by-Step Calculation:
-
Determine the distance from Earth’s center:
\(\displaystyle r = R + h = 6.38 \times 10^6 \, \text{m} + 10,000 \, \text{m} \approx 6.39 \times 10^6 \, \text{m}\) -
Compute the square of the distance:
\(\displaystyle r^2 = \left(6.39 \times 10^6 \, \text{m}\right)^2 = 4.08321 \times 10^{13} \, \text{m}^2\) -
Calculate the product of the masses:
\(\displaystyle m_1 m_2 = 5.98 \times 10^{27} \, \text{kg}^2\) -
Apply the gravitational force formula:
\(\displaystyle F = G \frac{m_1 m_2}{r^2} = \left(6.67 \times 10^{-11}\right) \frac{5.98 \times 10^{27}}{4.08321 \times 10^{13}}\) -
Perform the calculation:
\(\displaystyle F \approx 9.755 \times 10^3 \, \text{N}\)
Answer: At an altitude of 10,000 meters, the gravitational force is approximately \( 9755 \, \text{N} \). The slight decrease in force compared to the surface is due to the increased distance from the Earth's center.
9. Frequently Asked Questions (FAQ)
Q1: Why is gravity considered a "weak" force?
Even though gravity dominates on astronomical scales, it is the weakest among the four fundamental forces (electromagnetic, strong nuclear, weak nuclear, and gravitational). When comparing two small objects, the gravitational force is minuscule relative to electromagnetic forces. However, because gravity is always attractive and acts cumulatively over large masses, it becomes the dominant force in celestial mechanics.
Q2: How did Newton derive his law of universal gravitation?
Newton’s derivation was based on observational evidence—such as the falling apple and the motion of celestial bodies—and on the mathematical insights provided by Kepler’s laws of planetary motion. Newton recognized that the force causing objects to fall on Earth was the same force governing the motion of the Moon and planets, leading to the formulation of his universal law.
Q3: How does the inverse square law work in gravity?
The inverse square law indicates that the gravitational force diminishes with the square of the distance between two masses. For example, if the distance is doubled, the force becomes:
\(\displaystyle F \propto \frac{1}{(2r)^2} = \frac{1}{4r^2}\)
This rapid decrease is why distant celestial objects have a much weaker gravitational influence on us.
Q4: What role does the gravitational constant \( G \) play?
The constant \( G \) calibrates the gravitational force equation, ensuring that the formula is consistent and applicable across all scales. Its precise value, measured by experiments like Cavendish’s torsion balance, allows scientists to calculate gravitational interactions accurately—from determining the weight of objects to plotting the trajectories of spacecraft.
Q5: How does gravity affect satellites and space probes?
Satellites and space probes are placed into orbits where their tangential velocity balances the gravitational pull of a planet or star. This balance keeps them in stable orbits, preventing them from either falling into the planet or escaping into space. Precise calculations based on Newton’s law ensure successful satellite deployment and space mission planning.
10. Summary and Conclusion
Gravity is more than just a force that pulls objects to the ground—it is a fundamental interaction that shapes the universe. From Newton’s revolutionary insights to the modern applications of gravitational physics in space exploration, understanding gravity is essential for both scientific inquiry and everyday life.
Key Takeaways:
- Universal Attraction: Gravity acts between any two objects with mass, regardless of their size or distance.
-
Newton’s Law: The gravitational force is expressed as
\(\displaystyle F = G \frac{m_1 m_2}{r^2}\)
highlighting the dependence on both mass and distance. - Inverse Square Law: The force diminishes rapidly with increased distance, explaining the varying gravitational effects experienced on Earth and in space.
- Historical Impact: Newton’s formulation, later refined by experiments such as Cavendish’s, unified terrestrial and celestial mechanics.
- Orbital Dynamics: Gravity, balanced by the inertia of tangential motion, keeps planets, moons, and satellites in their orbits.
- Real-World Applications: From weight measurement to satellite deployment and tidal energy, the principles of gravity are integral to our daily lives and technological progress.
Advances in gravitational physics, such as studies of gravitational waves and the search for dark matter, continue to deepen our understanding of this fundamental force. As technology progresses, we can expect new discoveries that further illuminate how gravity shapes our universe—from the smallest particles to the vast expanses of space.
Embracing the beauty and complexity of gravity not only enhances our knowledge of physics but also inspires our exploration of the vast universe that surrounds us.
Bubble Pop, Memory Match, Endless Alphabet & Panda Pop
In today’s digital age, mobile games have become more than just a source of entertainment—they’ve evolved into powerful learning tools that can significantly impact a child’s cognitive development. Among the vast array of free games available, four stand out for their engaging gameplay and educational benefits: Bubble Pop Game, Memory Match Game, Endless Alphabet Game, and Panda Pop Game. These free learning games offer more than just fun; they provide crucial developmental advantages that can enhance a child’s memory, problem-solving skills, and overall cognitive abilities.
The Hidden Educational Power of Mobile Games
Before diving into the specifics of each game, it’s important to understand why these seemingly simple entertainment apps have garnered attention from parents, educators, and child development experts alike. The convergence of play and learning creates an environment where children absorb knowledge without the pressure or boredom sometimes associated with traditional learning methods.
Mobile games tap into the brain’s reward system, releasing dopamine when players accomplish goals or overcome challenges. This natural reward mechanism creates a positive association with learning, encouraging children to continue engaging with educational content. It’s a perfect example of how free courses of learning can be embedded into everyday play.
Bubble Pop Game: More Than Just Popping Bubbles
What Makes Bubble Pop Games Special?
Bubble Pop Game variants have dominated the casual mobile gaming scene for years, and for good reason. The premise is simple: players match colorful bubbles to clear them from the screen. However, beneath this straightforward concept lies a complex web of cognitive benefits.
Cognitive Benefits for Growing Minds
When children engage with Bubble Pop Game mechanics, they’re actually exercising several critical mental functions:
- Color Recognition and Matching: The fundamental gameplay requires identifying and matching colors, a basic cognitive skill that forms the foundation for more complex learning.
- Strategic Thinking: As levels progress, children must develop strategies to clear bubbles efficiently, promoting forward-thinking and planning.
- Spatial Awareness: Bubble placement requires understanding of how objects interact in a defined space—a crucial developmental skill.
- Hand-Eye Coordination: The timing and precision needed to aim and shoot bubbles enhances fine motor skills and coordination.
Top Bubble Pop Games for Different Age Groups
For toddlers (ages 2-4):
- Bubble Pop Baby Games: Simplified mechanics with bright colors and rewarding sound effects
- Baby Bubble Pop: Features large, easy-to-tap bubbles with animal sounds
For preschoolers (ages 4-6):
- Bubble Shooter for Kids: Introduces basic matching concepts with guided play
- Tiny Bubbles: Teaches color mixing principles alongside bubble popping
For elementary school children (ages 6-12):
- Bubble Witch 3 Saga: Adds narrative elements while maintaining the educational core
- Bubble Shooter Rainbow: Incorporates more complex color patterns and strategies
Real-World Skills Developed Through Bubble Games
The skills cultivated through Bubble Pop Game play extend beyond the screen:
- Pattern Recognition: Essential for mathematics and reading
- Decision-Making Under Pressure: Valuable for everyday problem-solving
- Resilience Through Repetition: Learning to persist despite challenges
Memory Match Game: Training Young Brains for Information Retention
The Science Behind Memory Games
Memory Match Game formats leverage the psychological principle of spaced repetition—a learning technique that involves reviewing information at gradually increasing intervals. This method has been proven to enhance long-term memory retention.
How Memory Match Enhances Cognitive Development
The simple act of flipping virtual cards and remembering their positions engages multiple cognitive processes:
- Working Memory Exercise: Children must hold information temporarily while processing other cards.
- Visual Processing Enhancement: Recognizing and remembering images strengthens visual discrimination abilities.
- Attention Span Extension: The need to focus on the game naturally increases concentration duration.
- Conceptual Categorization: More advanced Memory Match Games that group cards by themes help children develop categorization skills.
Memory Match Variations for Different Learning Styles
Visual learners:
- Photo Memory Match: Uses realistic images of objects, animals, or places
- Shape and Color Match: Focuses on geometric patterns and color combinations
Auditory learners:
- Sound Memory Match: Pairs identical sounds instead of images
- Musical Memory: Matches musical instruments or notes
Kinesthetic learners:
- Action Memory Match: Combines physical movements with card matching
- Touch-Sensitive Memory Games: Provides tactile feedback when matches are made
Memory Match as a Tool for Academic Skills
The versatility of Memory Match Game formats makes them ideal vehicles for academic content:
- Alphabet Matching: Pairs uppercase and lowercase letters
- Numerical Matching: Connects numbers with the corresponding quantity of objects
- Vocabulary Building: Matches words with their visual representations
- Foreign Language Acquisition: Pairs words in different languages
Creating Custom Memory Match Experiences
Many free learning apps allow for customization, enabling parents and educators to create personalized Memory Match Game experiences that target specific learning objectives:
- Family Photo Memory: Using familiar faces to engage younger children
- Current Curriculum Match: Incorporating content from school lessons
- Interest-Based Matching: Focusing on topics that excite the individual child
Endless Alphabet Game: Transforming Literacy Learning
Revolutionary Approach to Letter Recognition
The Endless Alphabet Game has transformed how children approach the fundamentally important task of learning letters and words. Instead of rote memorization, this innovative app brings letters to life through animation and interactivity.
The Mechanics of Playful Literacy
The genius of the Endless Alphabet Game lies in its multi-sensory approach:
- Interactive Letter Placement: Children drag animated characters (letters) into their correct positions.
- Phonetic Sound Reinforcement: Each letter makes its phonetic sound when touched, reinforcing sound-symbol relationships.
- Word Animation: Completed words trigger humorous animations that illustrate the word’s meaning.
- Vocabulary Expansion: The game introduces words beyond the typical preschool vocabulary, enriching language exposure.
Developmental Milestones Supported by Alphabetic Play
The Endless Alphabet Game supports multiple developmental milestones:
- Pre-Reading Skills: Foundational phonemic awareness and letter recognition
- Fine Motor Development: Precision required for letter dragging and placement
- Vocabulary Acquisition: Exposure to rich, varied vocabulary with context
- Sequential Processing: Understanding the correct order of letters in words
Beyond Basic Literacy: Advanced Features
The educational depth of the Endless Alphabet Game extends beyond basic letter recognition:
- Word Categorization: Words are often thematically grouped, building conceptual understanding
- Contextual Learning: Animations provide context clues about word meanings
- Morphological Awareness: Exposure to prefixes, suffixes, and word roots in more advanced words
- Pronunciation Models: Clear audio pronunciation models support speech development
Integrating Endless Alphabet into Daily Learning Routines
The Endless Alphabet Game’s flexibility makes it ideal for integration into daily routines:
- Morning Alphabet Practice: Starting the day with a few words builds positive learning momentum
- Travel Companion: Turning transit time into productive learning opportunities
- Bedtime Wind-Down: A calmer alternative to more stimulating games before sleep
- Vocabulary Boost: Targeted use to support words encountered in books or conversation
Panda Pop Game: Strategic Thinking in Disguise
The Captivating World of Panda Pop
While the cute panda characters and colorful bubbles might seem purely entertainment-focused, Panda Pop Game mechanics incorporate sophisticated problem-solving elements that challenge developing minds.
Cognitive Challenges Hidden in Cute Packaging
The Panda Pop Game offers several cognitive challenges:
- Physics-Based Problem Solving: Understanding how bubbles will interact based on trajectory and momentum.
- Resource Management: Limited bubbles require thoughtful use of available resources.
- Goal Prioritization: Multiple objectives within levels teach prioritization skills.
- Adaptive Strategy Development: Changing level designs require flexible thinking and strategy adaptation.
Mathematical Concepts Embedded in Gameplay
The Panda Pop Game subtly incorporates mathematical thinking:
- Geometric Principles: Angle calculation for optimal bubble placement
- Probability Assessment: Predicting likely outcomes of various moves
- Numerical Progression: Understanding level progression and scoring systems
- Set Theory Basics: Grouping similar items (bubbles of the same color)
Problem-Solving Approaches Developed Through Play
Regular engagement with Panda Pop Game challenges promotes several problem-solving approaches:
- Trial and Error Learning: Testing strategies and learning from results
- Pattern Recognition: Identifying recurring level designs and optimal solutions
- Decomposition Skills: Breaking complex levels into manageable sections
- Algorithmic Thinking: Developing step-by-step approaches to challenges
Social and Emotional Learning Through Panda Pop
Beyond cognitive benefits, the Panda Pop Game format offers opportunities for social-emotional development:
- Frustration Tolerance: Learning to persist through challenging levels
- Achievement Recognition: Celebrating milestones and accomplishments
- Community Participation: Many versions include team challenges or friend interactions
- Emotional Regulation: Managing the excitement of success and disappointment of setbacks
The Intersection of Free Games and Quality Learning
Breaking Down the Cost Barrier to Education
One of the most significant advantages of games like Bubble Pop Game, Memory Match Game, Endless Alphabet Game, and Panda Pop Game is their accessibility. These free games demolish financial barriers to quality learning experiences, democratizing educational content.
The Free Learning Revolution in Mobile Gaming
The availability of high-quality free learning opportunities through gaming represents a revolution in educational access:
- Universal Access: Children across socioeconomic backgrounds can access identical learning content.
- Supplemental Education: Free games provide additional learning opportunities beyond formal education.
- Differentiated Learning Paths: Various game types address different learning styles and needs without additional cost.
- Continuous Content Updates: Many free games regularly update content, providing fresh learning challenges.
Evaluating Quality in Free Educational Games
Not all free games offer equal educational value. Parents and educators should consider these factors when selecting free learning games:
- Developmental Appropriateness: Content matched to the child’s current abilities with room for growth
- Learning Integration: Educational elements seamlessly woven into enjoyable gameplay
- Engagement Sustainability: Ability to maintain interest beyond novelty period
- Progress Measurement: Features that track development and mastery
- Ethical Design: Absence of manipulative monetization tactics or inappropriate content
Monetization Models and Educational Integrity
Understanding how free games are monetized helps assess their educational integrity:
- Ad-Supported Models: Consider frequency, content, and placement of advertisements
- Freemium Approaches: Evaluate whether core educational content is truly accessible without payment
- Data Collection Practices: Review privacy policies regarding information gathered from young users
- Premium Content Balance: Determine if non-paying users still receive substantial educational value
Integrating Educational Games into Balanced Development
Creating a Holistic Digital Learning Environment
While games like Bubble Pop Game, Memory Match Game, Endless Alphabet Game, and Panda Pop Game offer tremendous benefits, they work best as part of a balanced approach to child development.
Screen Time Guidelines for Educational Gaming
Research-based recommendations for educational game time include:
- Age-Appropriate Limits: Following pediatric guidelines for total screen time
- Co-Play Sessions: Adult participation enhances learning transfer
- Natural Stopping Points: Respecting attention span limitations rather than enforcing arbitrary time limits
- Balance Indicators: Monitoring for signs that digital play is displacing other essential activities
Complementary Non-Digital Activities
To maximize the benefits of educational games, pair them with related offline activities:
For Bubble Pop Game:
- Physical bubble-blowing and popping
- Color sorting games with household objects
- Target practice activities for hand-eye coordination
For Memory Match Game:
- Traditional physical memory card games
- Scavenger hunts with memory elements
- “What’s missing?” observation games
For Endless Alphabet Game:
- Letter formation with clay or finger paints
- Sound scavenger hunts (finding objects that start with specific sounds)
- Storytelling incorporating newly learned vocabulary
For Panda Pop Game:
- Strategy board games appropriate for age
- Building challenges with blocks or construction toys
- Puzzle-solving activities of increasing complexity
Monitoring and Supporting Progress
Effective integration of educational games involves ongoing assessment and support:
- Observational Assessment: Noting which skills seem to be developing through gameplay
- Conversation Integration: Discussing game concepts during everyday activities
- Challenge Calibration: Ensuring the child is appropriately challenged but not frustrated
- Interest Expansion: Using game topics as springboards to broader learning
The Future of Educational Gaming
Emerging Technologies Enhancing Learning Games
The educational potential of games like Bubble Pop Game, Memory Match Game, Endless Alphabet Game, and Panda Pop Game continues to expand with technological advancements:
- Augmented Reality Integration: Blending physical environments with digital game elements
- Adaptive Learning Algorithms: Customizing difficulty and content based on individual performance
- Voice Recognition Components: Adding spoken language elements to gameplay
- Cross-Platform Continuity: Seamless learning experiences across multiple devices
Personalized Learning Pathways
The future of educational gaming points toward increasingly personalized experiences:
- Learning Style Adaptation: Games that detect and adjust to individual learning preferences
- Progress-Based Content Delivery: Just-in-time learning materials based on demonstrated mastery
- Interest-Driven Branching: Content paths that follow the child’s curiosity
- Strength and Challenge Identification: Analytics that identify areas of proficiency and growth opportunity
Research-Informed Game Development
As researchers continue to study the impact of games on learning, we can expect developments in:
- Cognitive Load Optimization: Game design that maximizes learning while minimizing mental fatigue
- Transfer Effect Enhancement: Features that improve the application of game-learned skills to real-world situations
- Attention Management Mechanisms: Elements that support healthy attention development rather than exploiting attention vulnerabilities
- Social Learning Integration: Multiplayer educational experiences that leverage peer learning effects
Conclusion: The Lasting Impact of Educational Gaming
The seemingly simple activities found in Bubble Pop Game, Memory Match Game, Endless Alphabet Game, and Panda Pop Game represent a profound shift in how we approach early childhood education. These free games and free learning opportunities remove barriers to quality educational experiences while embedding crucial developmental support in engaging play.
As parents, educators, and caregivers navigate the complex landscape of children’s media, these educational games stand out as valuable tools that respect both the child’s need for enjoyment and their capacity for growth. The skills developed—from memory enhancement and strategic thinking to literacy foundations and problem-solving approaches—establish cognitive frameworks that support lifelong learning.
The true power of these games lies not just in their individual benefits but in their collective contribution to a child’s developing mind. When thoughtfully integrated into a balanced approach to learning and development, Bubble Pop Game, Memory Match Game, Endless Alphabet Game, and Panda Pop Game become more than just free courses in disguise—they become catalysts for curiosity, confidence, and cognitive growth.
By understanding the educational mechanisms at work behind the colorful interfaces and engaging gameplay, adults can make informed choices about which games will best support specific developmental needs while providing the joy and engagement that makes learning stick. In the expanding universe of digital media competing for children’s attention, these educational games represent some of the brightest stars—illuminating paths to knowledge through the simple, universal language of play.
FAQs About Educational Mobile Games
Are free games as educational as paid options?
Many free games offer educational value comparable to paid alternatives. The key factors are the game’s design principles and learning integration rather than price point. Some free games supported by reputable educational organizations may actually offer superior learning experiences compared to certain paid options.
How much time should children spend on educational games daily?
The American Academy of Pediatrics recommends that children ages 2-5 limit screen time to 1 hour per day of high-quality programming, while children 6 and older should have consistent limits on screen time in general. Within these guidelines, educational games like Bubble Pop Game, Memory Match Game, Endless Alphabet Game, and Panda Pop Game can form a valuable portion of the allocated time.
At what age should children start playing educational mobile games?
Most developmental experts recommend limiting screen exposure for children under 18-24 months, except for video chatting. Between ages 2-5, carefully selected educational games with adult participation can be introduced in limited durations. The games discussed in this article vary in appropriate starting ages, with simplified versions of Memory Match Game potentially suitable for children as young as 2, while Panda Pop Game might be more appropriate for children 4 and older.
How can I tell if a game is truly educational?
Look for games that:
- Clearly state learning objectives
- Integrate learning naturally into gameplay rather than as separate “educational” sections
- Provide appropriate challenges that adapt to skill level
- Offer meaningful feedback beyond simple “right/wrong” responses
- Avoid excessive rewards for minimal effort
- Come from developers with educational expertise or partnerships
Can these games help children with learning differences?
Yes, games like Bubble Pop Game, Memory Match Game, Endless Alphabet Game, and Panda Pop Game often provide multi-sensory learning experiences that can benefit children with various learning differences. The self-paced nature, immediate feedback, repetition without judgment, and multiple modes of interaction make them valuable tools for diverse learners. However, games should be selected with the specific child’s needs in mind, and it’s often helpful to consult with educational specialists for recommendations.