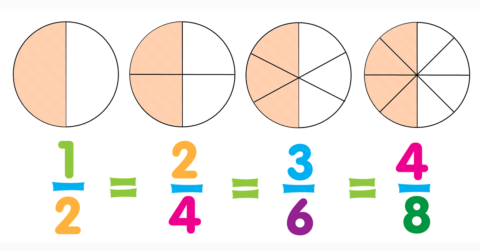Have you ever found yourself struggling to figure out how to combine pieces of a recipe, or wondered how to accurately compare and order portions when they’re written in different forms? Imagine trying to plan a community event where every fraction of resources—from time allocations to ingredient measurements—must be perfectly calculated. Welcome to our in-depth guide on adding fractions and mixed numbers, ordering fractions from least to greatest, and subtracting fractions (including those with unlike denominators and mixed numbers). In this post, we will cover everything you need to know about these essential arithmetic operations, and show you why mastering these concepts is crucial for both academic success and everyday problem solving.
Throughout this comprehensive guide, we will explore:
- How to add fractions and mixed numbers seamlessly
- The method of ordering fractions from least to greatest
- Techniques for subtracting fractions with unlike denominators
- Strategies for subtracting unlike fractions and mixed numbers
- Practical examples and real-world applications of these skills
- Actionable tips, best practices, and common pitfalls to avoid
- A detailed FAQ section addressing frequently asked questions
- A call-to-action to further your mathematical journey
Whether you’re a student needing clarity on these topics, an educator looking for fresh ideas, or simply someone keen to enhance your numeracy skills, this post is designed just for you. Let’s embark on this journey to demystify the world of fractions and mixed numbers, ensuring that every part—no matter how small—fits perfectly into the whole.
Definition and Historical Background
In arithmetic, adding fractions and mixed numbers involves combining parts of a whole, while ordering fractions from least to greatest requires a comparison of these parts, and subtracting fractions with unlike denominators and mixed numbers involves determining the difference between these parts. More specifically:
- Adding Fractions and Mixed Numbers: To add fractions, they must share a common denominator. When adding mixed numbers, you often convert them to improper fractions first. For example, to add \( \frac{1}{4} \) and \( \frac{1}{3} \), you would find a common denominator, such as 12, and write them as \( \frac{3}{12} \) and \( \frac{4}{12} \), respectively. The sum is then \( \frac{3+4}{12} = \frac{7}{12} \). For mixed numbers like \( 2\frac{1}{4} \) and \( 3\frac{2}{3} \), convert them to improper fractions, add, and if desired, convert back.
- Fraction Least to Greatest: Ordering fractions means arranging them in ascending order. This often requires converting each fraction to a common denominator or to decimal form to compare sizes accurately.
- Subtracting Fractions with Unlike Denominators: Similar to addition, subtraction of fractions with different denominators requires finding a common denominator. For example, subtracting \( \frac{2}{5} \) from \( \frac{3}{4} \) involves converting both to a common denominator (e.g., 20) before performing the subtraction.
- Subtracting Unlike Fractions and Mixed Numbers: This process involves similar steps—first, ensuring the fractions have a common denominator, and then subtracting the numerators. When mixed numbers are involved, they are often converted to improper fractions for easier manipulation.
Historically, the concept of fractions dates back to ancient civilizations such as the Egyptians and Babylonians, who used fractions for trade, land measurement, and astronomy. Over time, methods for handling fractions evolved, leading to the sophisticated arithmetic rules we use today. The systematic approach to adding, subtracting, and ordering fractions was refined during the Renaissance period, paving the way for modern algebra and calculus.
For more historical context, visit reputable sources such as Wikipedia: Fraction (Mathematics) or explore interactive lessons on Khan Academy.
Adding Fractions and Mixed Numbers
The process of adding fractions begins with ensuring that the fractions have a common denominator. If the denominators are the same, you simply add the numerators and keep the common denominator. For example:
\( \frac{1}{4} + \frac{1}{4} = \frac{1+1}{4} = \frac{2}{4} = \frac{1}{2} \)
However, when working with mixed numbers, the process involves an extra step. Consider the mixed numbers \( 2\frac{1}{4} \) and \( 3\frac{2}{3} \). The first step is to convert them into improper fractions:
\( 2\frac{1}{4} = \frac{2 \times 4 + 1}{4} = \frac{9}{4} \)
\( 3\frac{2}{3} = \frac{3 \times 3 + 2}{3} = \frac{11}{3} \)
Next, find a common denominator. For \( \frac{9}{4} \) and \( \frac{11}{3} \), the least common denominator (LCD) is 12:
\( \frac{9}{4} = \frac{9 \times 3}{4 \times 3} = \frac{27}{12} \)
\( \frac{11}{3} = \frac{11 \times 4}{3 \times 4} = \frac{44}{12} \)
Now, add the fractions:
\( \frac{27}{12} + \frac{44}{12} = \frac{27 + 44}{12} = \frac{71}{12} \)
The result \( \frac{71}{12} \) can be converted back to a mixed number if desired:
\( \frac{71}{12} = 5\frac{11}{12} \)
This detailed process of converting, finding a common denominator, and then adding applies to any situation where you are combining fractions or mixed numbers.
Real-World Application: In cooking, recipes often call for the addition of different fractional measurements. For instance, if one recipe requires \( \frac{1}{2} \) cup of oil and another requires \( \frac{1}{3} \) cup, converting them to a common denominator (e.g., \( \frac{3}{6} \) and \( \frac{2}{6} \)) allows you to add them easily, resulting in \( \frac{5}{6} \) cup of oil.
Ordering Fractions from Least to Greatest
Understanding how to order fractions—often referred to as arranging them from least to greatest—is an important skill. It allows you to compare parts of a whole and is especially useful in data analysis and real-world planning.
To order fractions, you typically convert them to have a common denominator or transform them into decimal form for easy comparison. For example, consider the fractions \( \frac{3}{5} \), \( \frac{1}{2} \), and \( \frac{4}{7} \).
One method is to convert each fraction into decimals:
- \( \frac{3}{5} \approx 0.60 \)
- \( \frac{1}{2} = 0.50 \)
- \( \frac{4}{7} \approx 0.57 \)
Once in decimal form, the order from least to greatest is:
\( 0.50 \) ( \( \frac{1}{2} \) ), \( 0.57 \) ( \( \frac{4}{7} \) ), \( 0.60 \) ( \( \frac{3}{5} \) )
Alternatively, you can find a common denominator to compare them directly. This skill is essential not only in academic contexts but also when you need to organize data or make decisions based on proportions.
Example in Real Life: When planning a budget, you might need to rank different expense categories by the fraction of the total budget they represent. Ordering these fractions from least to greatest helps in prioritizing expenses.
Subtracting Fractions with Unlike Denominators
Subtraction of fractions with unlike denominators follows a process very similar to addition. The key is to first obtain a common denominator before subtracting the numerators.
For example, consider subtracting \( \frac{2}{5} \) from \( \frac{3}{4} \). The denominators are 5 and 4, so the least common denominator is 20:
\( \frac{3}{4} = \frac{3 \times 5}{4 \times 5} = \frac{15}{20} \)
\( \frac{2}{5} = \frac{2 \times 4}{5 \times 4} = \frac{8}{20} \)
Now subtract the fractions:
\( \frac{15}{20} - \frac{8}{20} = \frac{15 - 8}{20} = \frac{7}{20} \)
This method ensures that the fractions represent parts of the same whole, making the subtraction straightforward.
Real-World Application: In construction, you might need to subtract measurements when determining the remaining length of a material after cutting a piece. Accurate subtraction of fractions ensures that the measurements are precise.
Subtracting Unlike Fractions and Mixed Numbers
Subtracting fractions becomes slightly more complex when mixed numbers are involved. The process typically requires you to convert mixed numbers to improper fractions before proceeding with the subtraction.
Consider the problem of subtracting \( 1\frac{3}{4} \) from \( 3\frac{2}{3} \). First, convert the mixed numbers:
\( 1\frac{3}{4} = \frac{1 \times 4 + 3}{4} = \frac{7}{4} \)
\( 3\frac{2}{3} = \frac{3 \times 3 + 2}{3} = \frac{11}{3} \)
Next, find the least common denominator for 4 and 3, which is 12:
\( \frac{7}{4} = \frac{7 \times 3}{4 \times 3} = \frac{21}{12} \)
\( \frac{11}{3} = \frac{11 \times 4}{3 \times 4} = \frac{44}{12} \)
Now, subtract the fractions:
\( \frac{44}{12} - \frac{21}{12} = \frac{44 - 21}{12} = \frac{23}{12} \)
You can leave the result as an improper fraction or convert it to a mixed number:
\( \frac{23}{12} = 1\frac{11}{12} \)
This approach—convert, find the common denominator, and subtract—ensures that you handle mixed numbers and unlike fractions with confidence.
Strategies for Ordering Fractions from Least to Greatest
Ordering fractions from least to greatest, sometimes phrased as fraction least to greatest, is a skill that involves comparing fractions accurately. Here are some strategies:
- Convert to Decimals: Convert each fraction into a decimal. This method is quick and works well when the fractions are simple. For example, \( \frac{3}{8} \approx 0.375 \), \( \frac{1}{2} = 0.5 \), and \( \frac{5}{8} \approx 0.625 \).
- Find a Common Denominator: When fractions share the same denominator, it is easy to see which is larger. For instance, if you have \( \frac{2}{7} \), \( \frac{3}{7} \), and \( \frac{1}{7} \), ordering them is as simple as comparing the numerators.
- Use Benchmark Fractions: Compare fractions to known benchmarks such as \( \frac{1}{2} \) or 1. This helps in quickly assessing the size of the fraction.
These strategies are not only useful in academic settings but also in real-life situations such as ranking priorities in budgeting or analyzing survey data.
Real-World Applications and Case Studies
The techniques for adding fractions and mixed numbers, ordering fractions from least to greatest, and subtracting fractions with unlike denominators are applied daily in numerous fields. Below are several case studies that illustrate these concepts in action:
Case Study 1: Recipe Adjustment for a Family Gathering
Consider a scenario where you have a recipe that calls for \( 1\frac{1}{2} \) cups of flour and \( \frac{3}{4} \) cup of sugar. If you need to adjust the recipe to serve more people, you must add and scale these fractions accurately. First, convert the mixed number:
\( 1\frac{1}{2} = \frac{3}{2} \)
If you decide to double the recipe, then you must multiply each fraction by 2:
\( 2 \times \frac{3}{2} = 3 \) cups of flour and \( 2 \times \frac{3}{4} = \frac{6}{4} = \frac{3}{2} \) cups of sugar.
If you then need to order these ingredients from least to greatest in terms of quantity, you convert them to a common format (in this case, both are mixed numbers or decimals) and compare. This real-life application underscores the importance of these skills in ensuring recipes are adjusted correctly.
Case Study 2: Budget Allocation in a Small Business
A small business owner needs to distribute a budget among various departments. Suppose \( \frac{2}{7} \) of the budget is allocated for marketing and \( \frac{3}{7} \) for operations. Ordering these fractions from least to greatest confirms that the smallest allocation is for a specific department and helps in planning:
\( \frac{2}{7} < \frac{3}{7} \)
Additionally, if a department later needs to reduce its expenditure by subtracting \( \frac{1}{5} \) of the budget from \( \frac{3}{7} \), the owner must convert these fractions to a common denominator before subtracting:
Convert \( \frac{3}{7} \) and \( \frac{1}{5} \) to a common denominator (35):
\( \frac{3}{7} = \frac{15}{35} \) and \( \frac{1}{5} = \frac{7}{35} \).
Subtraction yields \( \frac{15}{35} - \frac{7}{35} = \frac{8}{35} \).
This precise calculation ensures that the revised budget is both accurate and fair.
Case Study 3: Data Analysis in Educational Research
In educational research, survey data may involve fractions representing the proportions of students achieving certain grades. If one survey indicates that \( \frac{2}{5} \) of students passed an exam and another indicates \( \frac{1}{4} \) passed a supplementary test, researchers might need to subtract or add these fractions to analyze overall performance. Converting these fractions to a common denominator or decimals facilitates clear data interpretation and effective decision-making.
Actionable Tips, Strategies, and Best Practices
Whether you are adding fractions and mixed numbers, ordering fractions from least to greatest, or subtracting fractions with unlike denominators, here are some proven strategies to enhance your accuracy and efficiency:
- Convert Early: Always convert mixed numbers to improper fractions before performing addition or subtraction. This simplifies the process and minimizes errors.
- Find the LCD: For fractions with unlike denominators, invest time in finding the least common denominator. This not only makes addition and subtraction easier but also helps when ordering fractions.
- Use Visual Aids: Draw area models, number lines, or pie charts to visually represent fractions. Visualization is especially useful when comparing sizes or performing operations with fractions.
- Simplify Frequently: Always simplify your final answers. This makes it easier to compare fractions and check for accuracy.
- Practice Mental Math: With regular practice, you will develop a natural intuition for converting, ordering, adding, and subtracting fractions.
- Double-Check with Decimals: When in doubt, convert fractions to decimals to verify your results. This cross-checking method can help catch any miscalculations.
- Leverage Technology: Use online tools and interactive platforms like Khan Academy and Math is Fun for additional practice.
By following these strategies, you can build a strong foundation in fractional arithmetic that will benefit you in both academic and everyday contexts.
Frequently Asked Questions (FAQ)
Q1: Do I always need to convert mixed numbers to improper fractions?
A: While not always strictly necessary, converting mixed numbers to improper fractions simplifies the process of adding or subtracting fractions, especially when denominators differ.
Q2: How can I quickly find the least common denominator (LCD)?
A: You can find the LCD by determining the least common multiple (LCM) of the denominators. Listing the multiples or using prime factorization are effective methods.
Q3: What is the best way to order fractions from least to greatest?
A: Converting fractions to decimals or finding a common denominator are both effective strategies for ordering fractions accurately.
Q4: Why is it important to simplify fractions after performing operations?
A: Simplifying fractions helps in comparing values more easily and ensures that the results are presented in their simplest form for clarity.
Q5: Are there online resources for practicing these concepts?
A: Yes, websites like Khan Academy and Math is Fun provide interactive exercises and tutorials on fractions.
Q6: How do these skills apply to advanced mathematics?
A: A solid grasp of adding, ordering, and subtracting fractions lays the groundwork for more advanced topics in algebra, calculus, and statistics.
Additional Resources and Further Reading
To further enhance your understanding of fractional arithmetic, explore these valuable resources:
- Khan Academy: Fraction Arithmetic
- Math is Fun: Fractions
- Wikipedia: Fraction (Mathematics)
- National Council of Teachers of Mathematics (NCTM)
These sites offer interactive lessons, detailed explanations, and additional practice exercises that can further solidify your skills.
Recap and Final Encouragement
In this extensive guide, we have explored the essential topics of adding fractions and mixed numbers, ordering fractions from least to greatest, subtracting fractions with unlike denominators, and subtracting unlike fractions and mixed numbers. Here is a summary of what we covered:
- Adding Fractions and Mixed Numbers: Converting mixed numbers to improper fractions, finding common denominators, and performing the addition.
- Ordering Fractions: Strategies for comparing fractions by converting them to decimals or using common denominators.
- Subtracting Fractions with Unlike Denominators: The importance of finding a common denominator before subtracting.
- Subtracting Unlike Fractions and Mixed Numbers: Techniques to handle subtraction when mixed numbers are involved, ensuring accuracy through conversion and simplification.
- Practical Applications: Real-world examples from cooking, budgeting, construction, and research to demonstrate the importance of these skills.
- Actionable Tips and Best Practices: Strategies to build a strong foundation in fraction arithmetic.
- FAQ and Additional Resources: Answers to common questions and links to further reading and interactive tools.
Mastering these fractional operations not only enhances your academic skills but also equips you with the practical tools needed for everyday problem solving.
Every time you add, subtract, or order fractions, you are reinforcing a fundamental aspect of mathematics that underpins advanced topics and real-life applications.
Your Next Steps
Now that you have a comprehensive understanding of adding fractions and mixed numbers, fraction least to greatest, subtracting fractions with unlike denominators, subtracting unlike fractions and mixed numbers (and the related processes), it’s time to put your knowledge into practice:
- Review the techniques discussed and work through the exercises provided in this guide.
- Share this post with classmates, colleagues, or friends who might benefit from a refresher on fractional arithmetic.
- Explore the additional resources linked above for interactive lessons and further practice.
- Join online forums or study groups to discuss strategies and clarify doubts regarding fractions.
- Subscribe to our newsletter for more in-depth tutorials, tips, and the latest updates in mathematics education.
Every step you take toward mastering fractions builds a stronger foundation for your mathematical journey. So, what are you waiting for? Dive in, practice diligently, and share your success stories with others!
Final Thoughts
Mathematics is a never-ending journey of discovery and understanding. The skills of adding fractions and mixed numbers, ordering fractions from least to greatest, and subtracting fractions (even those with unlike denominators and mixed numbers) are not merely academic exercises; they are vital tools that help us make sense of the world around us.
Whether you are planning a meal, balancing a budget, or analyzing data, these fractional operations enable you to work with precision and confidence. Embrace the challenges, practice regularly, and remember that every small step you take in mastering these concepts contributes to your overall mathematical prowess.
Thank you for joining us on this comprehensive exploration. We hope this guide has not only clarified the process but also inspired you to delve deeper into the fascinating world of fractions.
Stay Connected and Keep Learning!
Your mathematical journey is important to us! Subscribe to our newsletter for regular updates, tutorials, and insightful articles that help you master everything from basic fractions to advanced calculus. Follow us on social media and join a community of enthusiastic learners who share tips, strategies, and success stories.
We value your feedback—let us know which topics you’d like us to cover next and share your own experiences with fractional arithmetic in the comments below.
Deep Dive: Advanced Topics and Further Exercises
For those eager to expand their knowledge beyond the basics, here are some advanced topics and exercises:
Advanced Topic 1: Adding and Subtracting Complex Mixed Numbers
Consider adding \( 4\frac{3}{8} \) and \( 5\frac{5}{6} \) or subtracting \( 7\frac{2}{5} \) from \( 9\frac{3}{4} \). Converting each mixed number to an improper fraction, finding a common denominator, and then performing the operation challenges your skills and reinforces the process.
Advanced Topic 2: Ordering Fractions in Data Sets
In statistics, you might encounter large data sets represented in fractions. Practice ordering fractions like \( \frac{5}{12} \), \( \frac{7}{15} \), \( \frac{9}{20} \), and \( \frac{4}{11} \) from least to greatest. Experiment with both the common denominator method and decimal conversion to see which works best for you.
Advanced Topic 3: Real-World Problem Solving
Create your own word problems that require adding, subtracting, and ordering fractions. For instance, design a scenario where a community center must divide resources among several programs, each represented by fractions. Solve the problem and reflect on how the techniques learned apply in a real-world context.
Practice Exercises
- Exercise: Add \( \frac{3}{8} \) and \( \frac{5}{12} \). Convert your answer into a mixed number.
- Exercise: Subtract \( 2\frac{1}{3} \) from \( 4\frac{3}{4} \) and simplify your result.
- Exercise: Order the fractions \( \frac{2}{7} \), \( \frac{5}{9} \), \( \frac{3}{8} \), and \( \frac{7}{10} \) from least to greatest.
- Exercise: Convert the following mixed numbers to improper fractions, then add and subtract as needed: \( 3\frac{1}{2} \), \( 2\frac{2}{3} \), and \( 1\frac{3}{4} \).
- Exercise: Write a brief essay on how mastering these techniques can help in everyday life, from cooking to budgeting.
Reflect on these exercises and discuss your findings with peers or mentors. The more you practice, the more intuitive these operations will become.