Interactive Surface Area Calculator – Find Surface Area Instantly
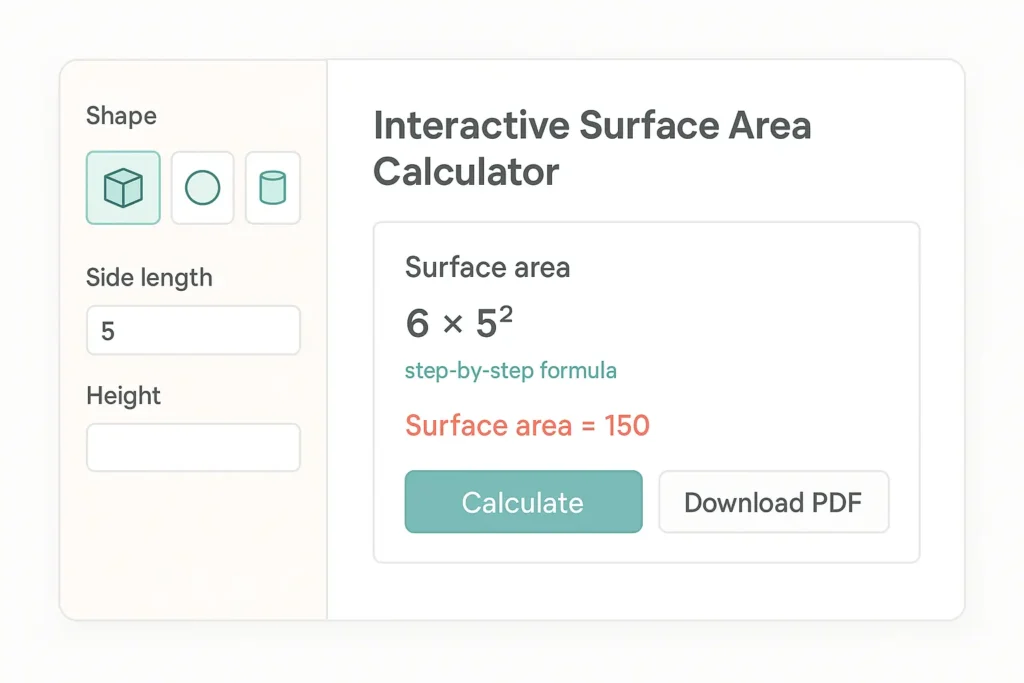
📐 Surface Area Calculator
Calculate the surface area of various 3D shapes
Please select a shape to see input fields
📊 Calculation Result
Surface Area Learning Tool
Surface Area Formulas
🟦 Cube
Where s = side length
SA = 6 × (5)² = 6 × 25 = 150 cm²
📦 Rectangular Prism
Where l=length, w=width, h=height
SA = 2(24 + 18 + 12) = 2(54) = 108 units²
⚪ Sphere
Where r = radius
SA = 4π(5)² = 4π(25) = 100π ≈ 314.16 cm²
🥫 Cylinder
Where r=radius, h=height
SA = 2π(9) + 2π(3)(8) = 18π + 48π = 66π ≈ 207.35 units²
🍦 Cone
Where r=radius, l=slant height
SA = π(16) + π(4)(6) = 16π + 24π = 40π ≈ 125.66 units²
Surface Area Flashcards
Surface Area Quiz
Test your knowledge with 12 random questions about surface area calculations!
🎉 Quiz Complete!
Understanding and Calculating Surface Area: FAQs
What is Surface Area? What is a Surface Area? What is the Surface Area?
Surface area is the total area that the surface of a three-dimensional object occupies. In simpler terms, it's the sum of the areas of all the faces (or surfaces) that enclose the 3D object.
Imagine you could "unwrap" a 3D shape and lay it flat; the surface area would be the total area of that flat pattern (called a net).
Surface area is measured in square units (e.g., cm2, m2, inches2, feet2).
This answers "what is surface area," "what is a surface area," and "what is the surface area."
How to Find Surface Area? How Do You Find Surface Area? How to Do Surface Area? How to Calculate Surface Area? How to Solve/Get/Figure Out Surface Area?
The general method to find the surface area of any 3D shape is to:
- Identify all the individual faces or surfaces that make up the object.
- Calculate the area of each of these individual faces/surfaces using appropriate 2D area formulas (e.g., area of a rectangle, triangle, circle).
- Sum the areas of all these faces/surfaces. The total sum is the surface area of the 3D object.
For common geometric shapes, there are specific formulas derived from this general principle.
This general approach covers "how to find surface area," "how do you find surface area," "how to calculate surface area," "how to do surface area," "how to solve surface area," "how to get surface area," "how do you do surface area," "how to figure surface area," "how can you find the surface area," "how to figure out surface area," "how to find the surface area," "how do you find the surface area," "how to compute surface area," "how do you calculate surface area," "how do you figure surface area," "how do i find surface area," "how to calculate surface are" (common typo), "how to calculate surface areas," and "how to determine surface area."
What is Total Surface Area? What is the Total Surface Area? How Do You Find the Total Surface Area?
Total Surface Area (TSA) refers to the sum of the areas of all surfaces of a three-dimensional object, including its base(s) and any curved surfaces.
It's essentially the same as "surface area" when referring to the entire outer area of a closed 3D shape. The term "total" is often used to distinguish it from "lateral surface area" (see below).
To find the total surface area, you use the general method of summing the areas of all faces, or apply the specific formula for the total surface area of that shape.
This answers "what is total surface area" and "what is the total surface area," "how do you find the total surface area."
What is Lateral Surface Area? What is a Lateral Surface Area? How to Find Lateral Surface Area?
Lateral Surface Area (LSA) refers to the area of all the side faces of a three-dimensional object, excluding the area of its base(s).
- For a prism or cylinder, it's the area of all faces except the top and bottom bases.
- For a pyramid or cone, it's the area of the sloping faces, excluding the base.
How to find lateral surface area:
- Identify only the lateral (side) faces of the object.
- Calculate the area of each lateral face.
- Sum these areas.
Alternatively, specific formulas exist for the LSA of common shapes.
This answers "what is a lateral surface area" and "what is lateral surface area," "how to find lateral surface area."
How to Calculate/Find Surface Area of a Rectangular Prism?
A rectangular prism has 6 rectangular faces. Let the length be l, width be w, and height be h.
- Area of top and bottom faces:
l × w(each) - Area of front and back faces:
l × h(each) - Area of side faces:
w × h(each)
Example: A rectangular prism has length = 5 cm, width = 3 cm, height = 2 cm.
SA = 2((5×3) + (5×2) + (3×2))
SA = 2(15 + 10 + 6)
SA = 2(31) = 62 cm2
This covers "how to calculate surface area of a rectangular prism," "how to find surface area of a rectangular prism," "how to find the surface area of a rectangular prism," "how to calculate the surface area of a rectangular prism," "how to find surface area of a rectangle prism," "how to find surface area of rectangular prism," "what is the surface area of a rectangular prism," "what is the surface area of the rectangular prism," "how do you calculate surface area of a rectangular prism," and "how to calculate surface area of a rectangle" (when referring to a 3D prism, not a 2D rectangle's area). "What is the surface area of this rectangular prism brainly" refers to a specific problem context.
How to Calculate/Find Surface Area of a Cube?
A cube is a special rectangular prism where all 6 faces are identical squares. Let the side length of the cube be s.
- Area of one face:
s × s = s2 - Since there are 6 identical faces:
Example: A cube has a side length of 4 cm.
SA = 6 × (4 cm)2 = 6 × 16 cm2 = 96 cm2
This answers "how to calculate surface area of a cube," "how to find surface area of a cube," "how to find the surface area of a cube," "how do you find the surface area of a cube," "how do you get the surface area of a cube," "what is the surface area of a cube," "how do i find the surface area of a cube," and "how to do surface area of a cube," "how to find surface area of cube."
How to Calculate/Find Surface Area of a Cylinder?
A cylinder has two circular bases and a curved lateral surface.
Let the radius of the base be r and the height of the cylinder be h.
- Area of one circular base:
πr2 - Area of two circular bases:
2πr2 - Lateral Surface Area (area of the curved side, which unrolls into a rectangle):
2πrh(Circumference × height)
or
SA = 2πr(r + h)
Example: A cylinder has a radius of 3 cm and a height of 7 cm.
SA = 2π(3)2 + 2π(3)(7)
SA = 2π(9) + 2π(21) = 18π + 42π = 60π cm2
Using π ≈ 3.14, SA ≈ 60 × 3.14 = 188.4 cm2
This addresses "how to calculate surface area of a cylinder," "how to find the surface area of a cylinder," "how to find surface area of a cylinder," "how do you find the surface area of a cylinder," "how to work out the surface area of a cylinder," "how to find surface area of cylinder," and "what is the surface area of a cylinder."
How to Calculate/Find Surface Area of a Sphere?
A sphere is a perfectly round three-dimensional object. Let its radius be r.
Example: A sphere has a radius of 5 cm.
SA = 4π(5 cm)2 = 4π(25 cm2) = 100π cm2
Using π ≈ 3.14, SA ≈ 100 × 3.14 = 314 cm2
This covers "how to find the surface area of a sphere," "how do you calculate the surface area of a sphere," "how to find surface area of sphere," "how to find the total surface area of a sphere," "how do i find the surface area of a sphere," "how do you find surface area of a sphere," "how to calculate surface area of a sphere," "how to do surface area of a sphere," and "how to find sphere surface area."
How to Calculate/Find Surface Area of a Cone?
A cone has a circular base and a curved lateral surface that tapers to a point (apex).
Let the radius of the base be r and the slant height be l (the distance from the apex to any point on the circumference of the base). The perpendicular height is h.
If you know r and h, you can find l using the Pythagorean theorem: l2 = r2 + h2, so l = √(r2 + h2).
- Area of the circular base:
πr2 - Lateral Surface Area (area of the curved sloping surface):
πrl
or
SA = πr(r + l)
Example: A cone has a radius of 4 cm and a slant height of 5 cm.
SA = π(4)2 + π(4)(5)
SA = 16π + 20π = 36π cm2
Using π ≈ 3.14, SA ≈ 36 × 3.14 = 113.04 cm2
This answers "how to find the surface area of a cone," "how do you find the surface area of a cone," "how to find surface area of a cone," and "how to get surface area of cone."
How to Calculate/Find Surface Area of a Pyramid?
The surface area of a pyramid is the sum of the area of its base and the areas of all its triangular lateral (side) faces.
For a Regular Pyramid (base is a regular polygon, and lateral faces are congruent isosceles triangles):
- Area of the Base (B): Calculate based on the shape of the base (e.g., square, equilateral triangle, regular pentagon).
- Lateral Surface Area (LSA):
- Area of one triangular face =
(1/2) × base_edge_of_triangle × slant_height_of_face. - LSA = Number of triangular faces × Area of one triangular face.
- Alternatively,
LSA = (1/2) × Perimeter_of_base × slant_height_of_pyramid_face (l). The slant height (l) here is the height of each triangular face.
- Area of one triangular face =
SA = B + (1/2)Pl
(P = perimeter of the base, l = slant height of a triangular face)
Example: Square Pyramid with base side 6 cm and slant height of a triangular face 5 cm.
Area of Base (B) = 6 × 6 = 36 cm2
Perimeter of Base (P) = 4 × 6 = 24 cm
LSA = (1/2) × 24 cm × 5 cm = 60 cm2
Total SA = 36 cm2 + 60 cm2 = 96 cm2
This covers "how to find the surface area of a pyramid," "how do you find the surface area of a pyramid," "how to find surface area of a pyramid," "how to find the surface area of a regular pyramid," and "how to find the surface area of a square pyramid."
How to Calculate/Find Surface Area of a Triangular Prism?
A triangular prism has two identical triangular bases and three rectangular lateral faces.
To find the total surface area:
- Calculate the area of one triangular base (B). You might use
(1/2) × base_of_triangle × height_of_triangle, or Heron's formula if you know all three sides of the triangle. - Area of two triangular bases =
2 × B. - Calculate the area of each of the three rectangular lateral faces. The length of each rectangle will be the height (or length) of the prism (
H), and the width of each rectangle will be one of the sides of the triangular base (let sides bes1,s2,s3).- Area of rectangle 1 =
s1 × H - Area of rectangle 2 =
s2 × H - Area of rectangle 3 =
s3 × H
- Area of rectangle 1 =
- Lateral Surface Area (LSA) =
(s1 + s2 + s3) × H = Perimeter_of_base × H. - Total Surface Area = Area of two bases + Lateral Surface Area.
SA = 2B + PH
This answers "how to find the surface area of a triangular prism," "how to find surface area of a triangular prism," "how to calculate the surface area of a triangular prism," "how do you find surface area of a triangular prism," "what is the surface area of a triangular prism."
How to Find the Surface Area of a Prism? (General Prism)
A prism is a 3D shape with two identical and parallel polygonal bases, and rectangular lateral faces connecting corresponding sides of the bases.
SA = 2B + PH
Where:
Bis the area of one of the polygonal bases.Pis the perimeter of one of the polygonal bases.His the perpendicular height of the prism (the distance between the two bases).
This general formula applies to rectangular prisms, triangular prisms, hexagonal prisms, etc.
This covers "how to find the surface area of a prism," "how do you find the surface area of a prism," and "how to do surface area of a prism," "how to find surface area of prism."
How to Find the Surface Area of a Triangle?
A triangle is a two-dimensional (2D) shape. It has area, but it does not have surface area in the same way a 3D object does. Surface area is a property of 3D objects.
If the question is asking for the area of a triangle, the most common formula is:
If the question mistakenly asks for "surface area of a triangle" when referring to a 3D object like a triangular prism or pyramid, then you would use the formulas for those shapes as described above.
This addresses "how to find the surface area of a triangle" and "how do you find the surface area of a triangle," which usually means the area of a 2D triangle.
Is Surface Area Cubed or Squared?
Surface area is a measure of area, which is two-dimensional. Therefore, surface area is always measured in square units (e.g., cm2, m2, inches2, feet2).
Volume is measured in cubed units (e.g., cm3, m3, inches3, feet3).
Other Specific Surface Area Questions
- "How does surface area of reactant particles affect reaction rate?" (Chemistry): Increasing the surface area of solid reactant particles generally increases the rate of a chemical reaction. This is because more particles are exposed and available to collide with other reactant particles, leading to more frequent successful collisions and thus a faster reaction. For example, a powder reacts faster than a solid lump of the same substance.
- "How to calculate body surface area (BSA)?" (Medicine): Body Surface Area (BSA) is a measurement used in medicine, often for drug dosage calculations (especially in chemotherapy). There are several formulas to estimate BSA, the most common being the Mosteller formula and the Du Bois formula. They typically use a person's height and weight.Mosteller Formula for BSA BSA (m2) = √[(Height(cm) × Weight(kg)) / 3600]Always use clinically validated formulas and consult medical professionals for dosage calculations. This answers "how to determine body surface area."
- "What are surface mount components (SMC)?" (Electronics): Surface Mount Components (SMCs) are electronic components designed to be mounted directly onto the surface of printed circuit boards (PCBs). This technology is called Surface Mount Technology (SMT). SMCs are typically smaller than their through-hole counterparts and allow for more automated and dense circuit board assembly.
- "What are surface tension?" / "What is surface tension?": Surface tension is a property of the surface of a liquid that allows it to resist an external force. It's due to the cohesive forces between liquid molecules. At the surface, molecules are not surrounded by like molecules on all sides (as they are in the bulk of the liquid), so they cohere more strongly to those directly associated with them on the surface. This creates a sort of "skin" or film on the liquid's surface, causing it to behave somewhat like a stretched elastic membrane (e.g., allowing small insects to walk on water, or water to form droplets).
Key Understanding: Calculating surface area involves finding the total area of all the exposed surfaces of a 3D object. Specific formulas make this easier for common geometric shapes, but the fundamental principle is to sum the areas of the individual faces.