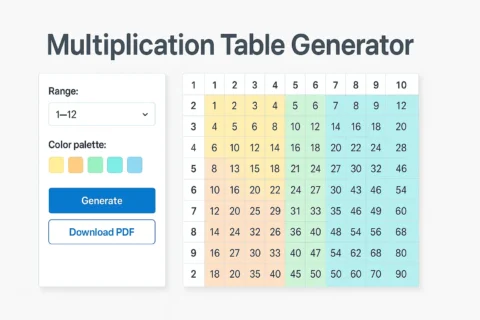
Advanced Multiplication Table
Table Configuration
Perfect Square
Prime Number
Special Multiple
Even Number
Odd Number
Table View
Learning Notes
| × | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 1 | 2 | 3 |
| 2 | 2 | 4 | 6 |
| 3 | 3 | 6 | 9 |
Mathematical Patterns in Multiplication Tables
Multiplication tables reveal many fascinating mathematical patterns:
- Perfect Squares: Numbers that are the product of a number multiplied by itself (e.g., 1×1=1, 2×2=4, 3×3=9). They form a diagonal line across the table.
- Commutative Property: The table demonstrates that a×b = b×a, creating a symmetry across the diagonal.
- Multiples: Each row and column shows the multiples of a particular number, revealing patterns in counting.
- Even and Odd Patterns: Products of two even numbers or two odd numbers are always even. The product of an even and odd number is always even.