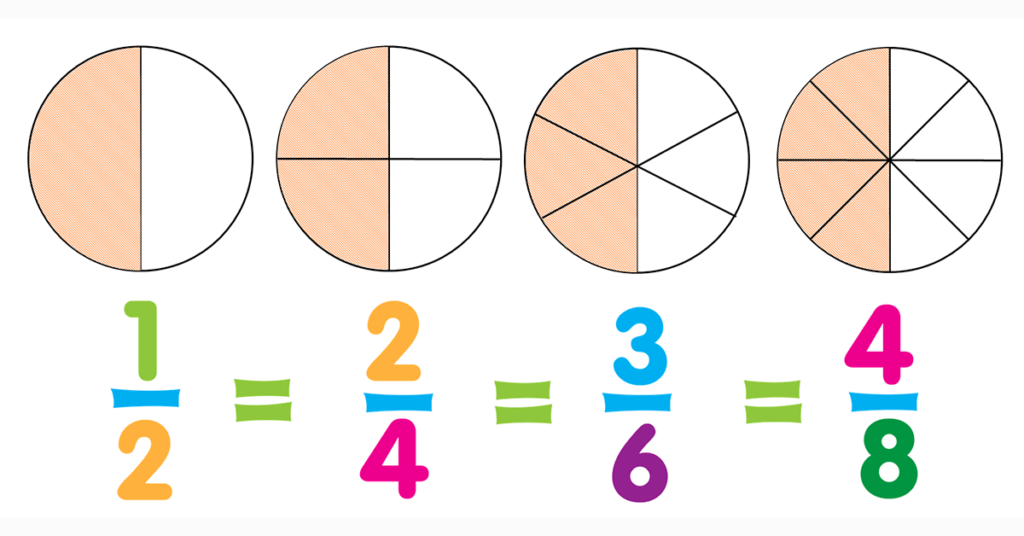Have you ever wondered why two seemingly different fractions can represent the exact same value? For instance, how is it possible that \( \frac{1}{2} \) is the same as \( \frac{2}{4} \) or \( \frac{50}{100} \)? In this blog post, we’ll embark on an enlightening journey to uncover the secrets of equivalent fractions. Whether you’re a student struggling with the basics, an educator looking for fresh ideas, or simply a curious mind eager to dive into the world of mathematics, you’ve come to the right place.
Introduction
Imagine slicing a delicious pizza into pieces: whether you cut it into 4, 6, or 8 slices, the overall size of the pizza remains the same. This everyday scenario is a perfect analogy for understanding equivalent fractions. In our day-to-day life, fractions play an essential role in cooking, budgeting, construction, and even in making critical decisions.
In this comprehensive guide, we’ll cover:
- The Definition of equivalent fractions
- Historical Background and how the concept evolved over time
- Detailed Explanations on how to identify, generate, and use equivalent fractions
- Real-World Examples and case studies that show the practical application of equivalent fractions
- Tips and Best Practices for mastering the concept in both academic and everyday contexts
- Frequently Asked Questions addressing common misconceptions and doubts
Understanding equivalent fractions is not just about passing a math test—it’s a fundamental skill that enhances your numerical literacy and problem-solving abilities. Ready to dive in? Let’s begin by exploring what equivalent fractions are all about!
What Are Equivalent Fractions?
At its core, equivalent fractions are fractions that, although they may have different numerators and denominators, represent the same value or proportion. In mathematical terms, two fractions \( \frac{a}{b} \) and \( \frac{c}{d} \) are equivalent if:
\( a \times d = b \times c \)
For example, consider the fractions \( \frac{1}{2} \) and \( \frac{2}{4} \). Using the definition above:
\( 1 \times 4 = 2 \times 2 \quad \text{or} \quad 4 = 4 \)
Since the equality holds true, these fractions are indeed equivalent.
A Brief Historical Perspective
The concept of fractions dates back thousands of years. Ancient civilizations, including the Egyptians and Babylonians, used fractions to divide land, resources, and in astronomical calculations. The Egyptians, for instance, had a unique method of representing fractions known as unit fractions (fractions with a numerator of 1) and their sums.
Over time, the understanding and notation of fractions evolved. In medieval Europe, mathematicians refined the way fractions were represented, making them more accessible and easier to manipulate. This evolution laid the groundwork for the modern arithmetic we study today, including the concept of equivalent fractions, which has become a cornerstone of basic mathematics.
Learn more about the fascinating history of fractions on History.com and Khan Academy.
Understanding the Concept of Equivalent Fractions
To truly grasp equivalent fractions, it’s important to understand the basics of fractions first. A fraction consists of a numerator (the top number) and a denominator (the bottom number). The numerator represents a part of the whole, while the denominator represents the total number of equal parts into which the whole is divided.
Equivalent fractions occur when different fractions represent the same part of a whole. For example, whether you see \( \frac{1}{2} \), \( \frac{2}{4} \), or \( \frac{50}{100} \), they all describe the same quantity—one half.
The secret behind equivalent fractions is the idea of multiplying or dividing both the numerator and the denominator by the same non-zero number. Consider the fraction \( \frac{1}{2} \). If you multiply both the numerator and the denominator by 3, you get:
\( \frac{1 \times 3}{2 \times 3} = \frac{3}{6} \)
Despite looking different, \( \frac{1}{2} \) and \( \frac{3}{6} \) are equivalent because they both represent the same portion of a whole.
This principle is foundational in mathematics and is applied in various areas, including algebra, calculus, and even in everyday reasoning. In the coming sections, we will explore practical methods to identify and generate equivalent fractions, and we will discuss their application in real-world scenarios.
Techniques for Finding Equivalent Fractions
There are several intuitive techniques to identify or generate equivalent fractions. Understanding these methods not only reinforces your grasp of fractions but also enhances your problem-solving skills. Here are some of the most effective techniques:
1. Multiplying or Dividing by the Same Number
The simplest method to create an equivalent fraction is by multiplying or dividing both the numerator and the denominator by the same number. For example:
-
Starting with \( \frac{2}{3} \), multiply both the numerator and denominator by 2:
\( \frac{2 \times 2}{3 \times 2} = \frac{4}{6} \) -
Similarly, if you start with \( \frac{3}{5} \) and multiply by 3:
\( \frac{3 \times 3}{5 \times 3} = \frac{9}{15} \) -
You can also reduce fractions by dividing by their greatest common divisor (GCD). For instance, \( \frac{8}{12} \) can be simplified by dividing both numbers by 4:
\( \frac{8 \div 4}{12 \div 4} = \frac{2}{3} \)
2. Using Cross-Multiplication
Cross-multiplication provides a quick way to check if two fractions are equivalent. For fractions \( \frac{a}{b} \) and \( \frac{c}{d} \), cross-multiplying means verifying if:
\( a \times d = b \times c \)
If the products are equal, the fractions are equivalent.
3. Visual Methods
Visual representations can be particularly helpful, especially for visual learners. Here are two effective visual techniques:
- Number Lines: Plot fractions on a number line to see if they land on the same point.
- Pie Charts or Bar Models: Divide a shape into equal parts and shade a fraction of it. By comparing different models, you can easily see that different fractions may cover the same area.
These techniques are not only useful in academic settings but also provide a solid foundation for understanding more advanced mathematical concepts.
Visualizing Equivalent Fractions
One of the best ways to internalize the concept of equivalent fractions is through visualization. Let’s explore several visual methods:
Using a Number Line
A number line is a straightforward tool for comparing fractions. When you plot fractions on a number line, you can easily see that fractions like \( \frac{1}{2} \), \( \frac{2}{4} \), and \( \frac{3}{6} \) all fall on the same point. This demonstrates their equivalence.
Consider the following illustration:
[A number line diagram showing equivalent points for \( \frac{1}{2} \), \( \frac{2}{4} \), and \( \frac{3}{6} \)]
Area Models
Area models use shapes like circles, rectangles, or squares divided into equal parts. For instance, if you have a circle divided into 4 equal parts and you shade 2 of them, you have represented \( \frac{2}{4} \) of the circle. Now, if you take a circle divided into 8 equal parts and shade 4, you again have half of the circle shaded, which represents \( \frac{4}{8} \).
This hands-on approach is especially effective for younger students or anyone who benefits from concrete, visual learning strategies.
Interactive Tools and Software
With modern technology, there are many interactive tools available online that allow you to manipulate fractions and see their equivalences in real time. Websites like Khan Academy and Math is Fun offer interactive modules that visually demonstrate how multiplying or dividing both the numerator and denominator by the same number yields an equivalent fraction.
By engaging with these visual tools, learners can build a stronger intuitive understanding of how equivalent fractions work, making the concept much easier to grasp.
Real-World Applications of Equivalent Fractions
Although the idea of equivalent fractions might seem abstract at first, it has numerous practical applications in everyday life. Let’s explore some scenarios where equivalent fractions play a crucial role:
Cooking and Recipes
When you’re cooking, recipes often require precise measurements. For example, if a recipe calls for \( \frac{1}{2} \) cup of milk, understanding that \( \frac{2}{4} \) or even \( \frac{3}{6} \) cup represents the same quantity can be incredibly useful if you only have measuring tools in different units. Adjusting recipes based on available tools or scaling recipes up or down relies heavily on your understanding of equivalent fractions.
Budgeting and Financial Planning
In finance, equivalent fractions can help when comparing different proportions. Whether you’re splitting expenses, calculating interest rates, or comparing discounts, understanding how different fractions relate to one another enables you to make better decisions. For example, knowing that \( \frac{25}{100} \) is equivalent to \( \frac{1}{4} \) can simplify calculations when comparing sale prices.
Measurement and Construction
In fields like construction or carpentry, precise measurements are vital. Contractors often need to convert fractions to ensure that measurements are accurate. For instance, a measurement of \( \frac{3}{8} \) of an inch might need to be converted into an equivalent fraction that is easier to work with, such as \( \frac{6}{16} \), depending on the tools available.
Everyday Decision-Making
Even in everyday situations like dividing a pizza among friends or sharing a bag of candy, understanding equivalent fractions can help ensure fairness. By quickly recognizing that \( \frac{2}{3} \) is equivalent to \( \frac{4}{6} \), you can split items into equal portions with confidence.
The more you understand equivalent fractions, the more naturally you will apply these concepts in a variety of situations, from academic settings to everyday life.
Tips and Best Practices for Mastering Equivalent Fractions
Whether you’re a student or an educator, mastering equivalent fractions can become much easier with the right strategies. Here are some actionable tips and best practices:
- Practice Regularly: Consistent practice with different fractions builds your confidence and familiarity with the concept. Use worksheets, online quizzes, or even cooking recipes to see fractions in action.
- Visualize the Concept: Use visual aids like number lines, pie charts, or fraction bars. Visualization not only reinforces the idea but also makes it easier to identify patterns.
- Break Down Problems: When faced with a complex fraction problem, break it down into smaller, manageable steps. Identify the greatest common divisor (GCD) or use cross-multiplication to verify equivalence.
- Use Real-World Examples: Apply the concept of equivalent fractions to everyday tasks such as cooking or budgeting. This real-world application cements the abstract ideas in a practical context.
- Collaborate and Teach Others: Explaining the concept to a friend or family member can deepen your own understanding. Teaching is a powerful tool for learning.
- Utilize Interactive Resources: Explore websites like Khan Academy or Math is Fun to reinforce your learning with interactive exercises and tutorials.
By incorporating these practices into your study routine, you’ll develop a robust understanding of equivalent fractions, making it easier to tackle more complex mathematical challenges in the future.
Case Studies and Practical Applications
To further illustrate the power of equivalent fractions, let’s take a look at a few detailed case studies that highlight how these concepts are applied in real-world situations.
Case Study 1: Adjusting a Recipe
Imagine you have a recipe that serves 4 people and requires \( \frac{3}{4} \) cup of sugar. However, you need to adjust the recipe to serve 8 people. Understanding equivalent fractions is essential here. By recognizing that doubling the recipe requires doubling the amount of each ingredient, you calculate:
\( \frac{3}{4} \times 2 = \frac{6}{4} \)
Then, by simplifying \( \frac{6}{4} \) (dividing numerator and denominator by 2), you find:
\( \frac{6 \div 2}{4 \div 2} = \frac{3}{2} \)
This tells you that you need \( \frac{3}{2} \) cups of sugar, or 1.5 cups, to serve 8 people. This simple adjustment, based on equivalent fractions, ensures that the taste and texture of the recipe remain consistent.
Case Study 2: Dividing Profits in Business
In a small business, profit sharing is often based on fractional ownership. Suppose three partners share profits in the ratio \( \frac{2}{5} \), \( \frac{3}{10} \), and \( \frac{1}{2} \). To fairly distribute the profits, it might be necessary to express these fractions with a common denominator. By converting them to equivalent fractions:
- \( \frac{2}{5} = \frac{4}{10} \) (multiply numerator and denominator by 2)
- \( \frac{3}{10} \) remains the same
- \( \frac{1}{2} = \frac{5}{10} \) (multiply numerator and denominator by 5)
The equivalent fractions \( \frac{4}{10} \), \( \frac{3}{10} \), and \( \frac{5}{10} \) clearly indicate that the profits will be split in a 4:3:5 ratio, ensuring transparency and fairness.
Case Study 3: Scaling in Construction
In construction, materials are often ordered in fractional quantities. For example, a contractor may need to scale a blueprint drawing. Suppose a wall’s length is represented as \( \frac{3}{4} \) of a drawing, but the actual wall is 12 feet long. To determine the scale factor and convert measurements accurately, the contractor uses equivalent fractions:
\( \frac{3}{4} = \frac{12}{x} \)
By cross-multiplying, the contractor finds:
\( 3x = 4 \times 12 \quad \Rightarrow \quad 3x = 48 \quad \Rightarrow \quad x = 16 \)
Thus, the full length of the wall in the drawing corresponds to 16 feet, and the equivalent fractions help in determining accurate scaling.
These case studies illustrate how equivalent fractions are not confined to textbooks—they are an indispensable tool in solving real-life problems.
Frequently Asked Questions (FAQ)
Q1: What exactly are equivalent fractions?
A: Equivalent fractions are fractions that represent the same value or proportion, even though their numerators and denominators are different. For example, \( \frac{1}{2} \) is equivalent to \( \frac{2}{4} \) because they both represent one half.
Q2: How do I determine if two fractions are equivalent?
A: One of the simplest methods is cross-multiplication. For fractions \( \frac{a}{b} \) and \( \frac{c}{d} \), if \( a \times d = b \times c \), then the fractions are equivalent.
Q3: Can I convert any fraction to an equivalent fraction?
A: Yes! You can multiply or divide both the numerator and the denominator of any fraction by the same non-zero number to obtain an equivalent fraction.
Q4: Why are equivalent fractions important in real life?
A: They are crucial for simplifying mathematical problems, comparing different quantities, and solving everyday problems—from cooking recipes to budgeting and scaling measurements in various fields.
Q5: What are some common mistakes when working with equivalent fractions?
A: Common errors include multiplying or dividing only the numerator or the denominator instead of both, or failing to simplify the fraction completely. Always ensure that the same operation is applied to both parts of the fraction.
Q6: Are there any interactive resources to practice equivalent fractions?
A: Absolutely! Websites such as Khan Academy and Math is Fun offer excellent interactive exercises and tutorials.
Additional Resources and Further Reading
If you’re eager to expand your knowledge about equivalent fractions and other mathematical concepts, here are some additional resources:
- Khan Academy: Fraction Arithmetic
- Math is Fun: Fractions
- Wikipedia: Fraction (Mathematics)
- National Council of Teachers of Mathematics (NCTM)
These resources provide in-depth lessons, interactive practice problems, and further insights into the fascinating world of fractions.
Conclusion
In summary, equivalent fractions are much more than a mere academic concept. They are a fundamental building block of mathematics that underpins many real-world applications—from cooking and construction to budgeting and decision-making. By understanding that fractions like \( \frac{1}{2} \), \( \frac{2}{4} \), and \( \frac{3}{6} \) are simply different representations of the same quantity, you unlock a new level of numerical literacy that can simplify complex problems.
We explored the definition and historical evolution of fractions, examined various techniques to identify and generate equivalent fractions, and delved into visual and interactive methods to solidify your understanding. Furthermore, real-world case studies demonstrated how these concepts are applied in practical scenarios, ensuring that you can see the relevance of equivalent fractions beyond the classroom.
Remember, mastering equivalent fractions not only sharpens your mathematical skills but also enhances your ability to analyze and solve everyday problems. Whether you are simplifying a recipe, splitting expenses, or scaling a project, the ability to work with equivalent fractions is an invaluable tool.
Now that you have a robust understanding of equivalent fractions, it’s time to put your knowledge into practice! We encourage you to revisit the interactive resources mentioned above, work on some practice problems, and even share this guide with friends and colleagues who might benefit from a refresher on this essential topic.
Call-to-Action: If you found this guide helpful, please leave your comments or feedback below. Share your own tips or stories about how understanding equivalent fractions made a difference in your life. And don’t forget to share this post on social media to help others unlock the mystery of fractional equality!
Final Thoughts
Mathematics is a language that describes the world around us, and equivalent fractions are one of its simplest yet most powerful expressions. By mastering this concept, you not only gain a better understanding of numbers but also cultivate problem-solving skills that will serve you in countless aspects of life.
As you continue on your mathematical journey, keep exploring, questioning, and applying what you learn. Remember, every fraction has a story, and every equivalent fraction is a reminder that sometimes, different perspectives can lead to the same beautiful truth.
Thank you for joining us on this deep dive into equivalent fractions. We hope you leave with a newfound appreciation for the elegance of mathematics and the endless possibilities it offers.
Stay Connected and Keep Learning!
If you enjoyed this post, be sure to subscribe to our newsletter for more in-depth explorations of mathematical concepts, educational tips, and interactive challenges. Follow us on social media and join our community of lifelong learners:
Your feedback is invaluable—drop a comment below, share your thoughts, and let us know which topics you’d like us to cover next!
Deep Dive: The Mathematics Behind Equivalent Fractions
For those eager to explore the mathematical intricacies of equivalent fractions further, let’s delve into some advanced aspects and thought-provoking questions:
The Role of Prime Factorization
One advanced method to understand why two fractions are equivalent involves prime factorization. By breaking down the numerator and denominator into their prime factors, you can simplify the fraction to its lowest terms. For example, consider the fraction \( \frac{8}{12} \):
- Prime factors of 8: \( 2 \times 2 \times 2 \)
- Prime factors of 12: \( 2 \times 2 \times 3 \)
Canceling the common factors (the two 2’s), we reduce the fraction to:
\( \frac{2}{3} \)
This process not only confirms that fractions can be equivalent in different forms but also emphasizes the importance of understanding the underlying structure of numbers.
Exploring Rational Numbers
Equivalent fractions are a subset of rational numbers—numbers that can be expressed as a fraction \( \frac{a}{b} \), where \( a \) and \( b \) are integers and \( b \neq 0 \). The study of rational numbers extends into algebra and number theory, where understanding equivalence classes is crucial. In this context, equivalent fractions are not just isolated examples; they are part of a broader framework that helps mathematicians explore properties of numbers and their relationships.
Applications in Algebra and Beyond
When dealing with algebraic expressions, the concept of equivalent fractions often surfaces in the process of simplifying expressions, solving equations, or integrating functions. Consider the expression:
\( \frac{2x}{4y} \)
Recognizing that this fraction can be simplified by dividing both the numerator and the denominator by 2 leads to:
\( \frac{x}{2y} \)
This simplification is not only useful in pure algebra but also plays a critical role in solving real-world problems involving rates, ratios, and proportional relationships.
As you continue to explore mathematics, keep in mind that mastering equivalent fractions opens doors to more advanced topics such as algebraic fractions, rational expressions, and even calculus.
Additional Exercises and Reflection
To solidify your understanding of equivalent fractions, here are some exercises and reflection prompts:
- Exercise 1: Write down five different fractions equivalent to \( \frac{3}{5} \) by multiplying the numerator and denominator by different integers.
- Exercise 2: Simplify the fraction \( \frac{18}{24} \) using both the greatest common divisor and prime factorization methods. Compare your results.
- Exercise 3: Create a number line and mark the positions of \( \frac{1}{2} \), \( \frac{2}{4} \), and \( \frac{3}{6} \). Write a short reflection on how this visualization helped you understand the concept better.
- Exercise 4: Think of a real-life scenario—like sharing a pizza or planning a road trip—and describe how equivalent fractions might be used to solve a problem in that scenario.
- Exercise 5: Research how fractions were used in ancient civilizations for trade or astronomy. Write a brief summary of your findings and how it relates to the concept of equivalent fractions.
Take your time with these exercises. Reflecting on and practicing the concept of equivalent fractions can help you build a deeper, more intuitive understanding of not only fractions but also the broader world of mathematics.
Recap and Final Encouragement
In this extensive exploration of equivalent fractions, we have journeyed from the fundamental definition to practical applications in everyday life. Here’s a quick recap of what we’ve covered:
- Definition: Equivalent fractions are fractions that represent the same value, as shown by the equality \( a \times d = b \times c \).
- Historical Context: The evolution of fractions from ancient civilizations to modern mathematics.
- Techniques: Methods such as multiplying/dividing by the same number, cross-multiplication, and visual strategies.
- Visualization: Using number lines, area models, and interactive tools to grasp the concept.
- Real-World Applications: Applying equivalent fractions in cooking, budgeting, construction, and more.
- Advanced Concepts: How equivalent fractions relate to algebra, prime factorization, and rational numbers.
- Exercises and Reflection: Hands-on activities to reinforce your understanding.
Remember, every time you simplify or compare fractions, you are practicing a fundamental skill that forms the backbone of mathematical thinking. Embrace the challenge, and don’t be afraid to experiment with different methods until you find the approach that works best for you.
We hope this guide has deepened your appreciation for the elegance and utility of equivalent fractions. As you continue to explore mathematics, keep in mind that every complex problem can be broken down into simpler, equivalent parts.
Your Next Steps
Are you ready to take your understanding of fractions to the next level? Here are a few steps to keep your momentum going:
- Revisit your class notes or textbooks and try simplifying fractions using the methods discussed.
- Challenge yourself with online quizzes and interactive exercises on websites like Khan Academy.
- Share this article with a friend or classmate who might benefit from a refresher on equivalent fractions.
- Join online forums or study groups where you can discuss and explore new mathematical ideas.
- Leave a comment below with your thoughts, questions, or personal experiences related to equivalent fractions.
Your journey through mathematics is a continuous adventure. Every new concept mastered builds a stronger foundation for future learning. So, what are you waiting for? Dive in, explore further, and share your newfound knowledge with the world!