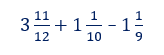Estimating is a skill first taught in KS1. It has many useful applications including checking answers, working with money and calculating area of irregular shapes. Estimating can also help children develop understanding the size of numbers. Questions on estimation are common and occur in most year groups.
What is estimation in maths?
To estimate in maths means to approximately calculate an answer. Some people may say it is a way to find a ‘rough’ or ‘near’ answer. There should be no need for calculators or written methods – even with larger or decimal numbers.
Why is it useful in maths?
Estimating is an essential skill. We use it in time, money, planning our day – what would life be like without estimating? Estimating is a skill that must be taught, not just assumed. We use estimating in day-to-day life.
Imagine you are in a shop and buying a coffee for £1.98, a chocolate bar for 49p and a pack of apples for 99p. It is likely that you would estimate the total cost to be £3.50.
We use estimating to make calculations faster, and easier, and when we are happy to find an answer close to the actual answer.
What are the rules for estimation?
In a calculation such as 4.78 x 6, understanding estimating can mean that 4.78 is rounded to 5. The new calculation of 5 x 6 can be solved almost instantly and give children a guide of what the actual answer should be.
This is also an excellent way of reinforcing understanding of place value. Teaching estimating in KS1 and helping children become fluent, makes a big difference in KS2 and beyond.
In primary school, children can use estimating to check their answers, compare calculations and estimate time. Later in life, estimating can be used professional contexts such as planning stages in engineering or time management.
What is an example of estimation?

Example taken from Year 4, Summer Term, Block 2, Step 4
How wrong can an estimate be?
Most estimates wouldn’t be considered wrong unless the difference between the estimated and actual answer is too great. The purpose of using estimation, is to find a near answer with little effort. Some estimated answers are better than others.
For example, the answer to the calculation 5,678 + 6,432 can be estimated by rounding the numbers to the nearest hundred (5,700 + 6,400 = 12,100) or to the nearest thousand (6,000 + 6,000 = 12,000). The actual answer is 12,110. Therefore, rounding to the nearest hundred gave the ‘better’ answer as it was nearest to the actual answer.
What is the disadvantage of an estimate?
If numbers are changed too much, the difference between the estimated and actual answer may be too large. This can be remedied by rounding to a sensible degree.
When is it used in primary school?
Estimating is used in Year 2 – 6 in many different contexts. It can be used in estimating length or capacity, to check an answer and much more.
Questions on estimation
White Rose Education have a wealth of maths resources available where you can find questions on estimation. You could try using our free schemes of learning and reasoning and problem-solving questions.
If you are a premium resources subscriber, you can find estimation related questions in our ‘Flashback 4s’ and small step PowerPoints, worksheets and videos.
Example questions on estimation:
1. A games console costs £429.85. In the January sale, there is a discount of 20%. Approximately, how much will the games console cost with the discount?
Approximately means to estimate. £429.85 could be rounded to £430 or £400
20% of £430 is £86 £430 – £86 = £344
20% of £400 is £80 £400 – £80 = £320
The discounted total would be approximately £344 or £320
The actual discounted total would be £343.88
2. A calculation that could be used to estimate the answer to:
To estimate an answer to this calculation, children should identify that these fractions are ‘close’ to a whole. An appropriate estimated calculation and answer could be 4 + 1 – 1 = 4
3. Estimate the answer to this calculation and then tick the actual answer.
6,789 x 11 = ?
- 74,679
- 57,789
- 89,999
- 6,789
Children can round 11 to 10 so the calculation can be done mentally. 6,789 x 10 = 67,890