On a scale of 7, 13 or 31 how much do you love prime numbers? Why is one not a prime number? What makes two the only even prime number? In this article we discuss the answers to these questions and learn about the fascinating properties of prime numbers.
Key takeaways
- A prime number is a whole number with exactly two factors: one and itself.
- The number one has only one factor and a prime number must have precisely two factors. Only having one factor is why one is not a prime number.
- Arrays can be used to illustrate the factors of a number.
What are prime numbers in maths?
Prime numbers are positive integers with exactly two distinct positive factors. The two factors of a prime are always one and the number itself. For example, seven is a prime number because the only factors are one and seven.
If a number has more than two factors, it is a composite number. For example, eight is a composite number because the factors are one, two, four and eight. The first, and smallest, prime number is two.
Prime numbers one to 100
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Even prime numbers
As we mentioned, two is a prime number because it has exactly two factors, one and two. Besides being the first prime, two is the only even prime number. All other even numbers have two as a factor, making them composite numbers.
How do you figure out if a number is prime?
To determine if a number is prime, list all its factors. If the number has exactly two factors, then it is prime. If a number has more than two factors it is a composite number.
Representing a prime number
Concrete, pictorial and abstract representations are an important part of developing a conceptual understanding of prime numbers. Arrays are a useful representation to illustrate the factors of a number.
Prime numbers only have one array representation – this is a single line of counters. The array can be horizontal, vertical or any orientation. It is the dimensions of the array that illustrate the factors of a number. A single line of counters represent one as a factor and the number itself.
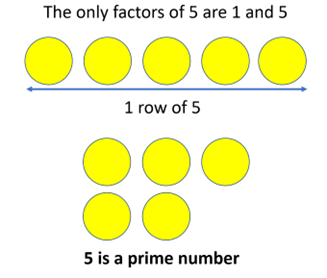
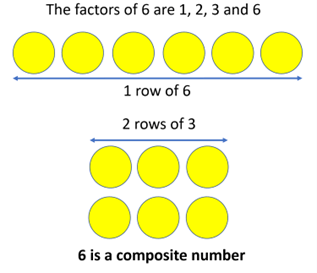
Five is prime as it only has one array, whereas six is a composite number since it has two or more arrays.
In Year 7, we explore arrays of numbers using counters in the Prime numbers & proof block.
What are the rules for prime numbers?
- Prime numbers are integers greater than one with exactly two distinct positive factors.
- The only even prime is two; all other even numbers are composite.
- Prime numbers greater than two are odd.
What is the fastest way to find prime numbers?
To find prime numbers, identify all the factors of a number. An efficient way is using factor pairs. Here are the first 10 positive integers with their factor pairs:
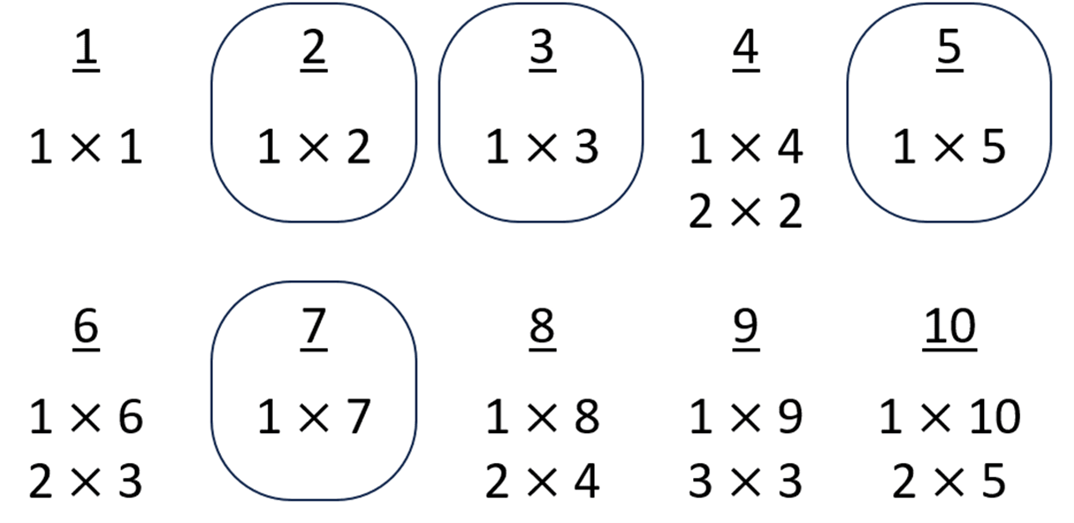
Be aware, factor pairs can cause misconceptions to arise. Here, one can be mistaken for having exactly two factors. However, notice that one is being multiplied by itself – making it the only factor. Since it has only one factor, one is not prime.
Notice also, four and nine only have three factors. Representing four as two rows of two counters illustrates that four is a square number, just like nine.
Are prime numbers hard to find?
As numbers increase, there are fewer prime numbers, this makes them harder to find. Rules of divisibility can be employed to identify primes more efficiently. Here are some examples:
7,314: Ends in a four so is an even number, meaning two is a factor. Therefore, 7,314 is not prime.
8,455: Ends in a five so is a multiple of five, meaning five is a factor. Therefore, 8,455 is not prime.
1,263: 1 + 2 + 6 + 3 = 12, 12 has three as a factor meaning 1,263 also has three as a factor. Therefore, 1,263 is not prime.
This reductive reasoning can make it easier to find prime numbers.
What is the best way to find a prime number?
One of the oldest and, to this day, most efficient methods for finding prime numbers up to a certain number, n, is to iteratively list all the multiples of each prime number. Then the unmarked values are primes.
We know this doesn’t feel fast, but it’s the best way to look for primes!
Some primes have certain patterns or special properties that can help identify them efficiently:
While there are many methods to find or identify prime numbers, for extremely large numbers it can be difficult for anyone to determine with absolute certainty.
Why one is not a prime number
One is not a prime number because of the role prime numbers play in the fundamental structure of mathematics. Primes are the building blocks of natural numbers; every positive integer can be uniquely expressed as a product of primes – this is known as prime factorization.
For example:
How do you prove one is not prime?
The proof that one is not prime lies in their definition. By definition, prime numbers are positive integers with exactly two factors: one and the number itself. Since one has only one factor – itself – it fails to meet the fundamental criteria.
Another perspective on this is that prime numbers are those that are divisible only by one and themselves.
As one is the exception in having only one factor, it is excluded from the category of prime numbers. This proof aligns with the conventional definition and properties of prime numbers in mathematics.
Example prime number questions
- Which number is the only even prime number?
- When you add together two prime numbers, do they always give an even number? Explain your answer.
- Which large numbers can you tell are not prime just by looking at their digits?
- You’re playing a raffle game, with tickets numbered 1 to 100. You can win a prize if you pick a ticket that meets one of these two criteria:
- Win a prize for a multiple of eight.
- Win a prize for a prime number.
Which criteria would you choose to have a better chance of winning? Explain why
In summary
Understanding the significance of prime numbers illuminates fundamental principles in mathematics. Through their definition as integers with precisely two factors, primes serve as the building blocks of natural numbers, essential for prime factorization. This underlines why one, with its sole factor, does not qualify as prime.
Meanwhile, exploring the properties and patterns of prime numbers enriches mathematical insight, from discerning Mersenne primes to the hunt for twin primes. While strategies exist for identifying primes, the inherent complexity of larger numbers stresses their challenging nature. Thus, exploring prime numbers unveils both the elegance and complex nature inherent in mathematics.








