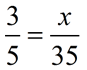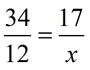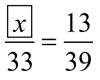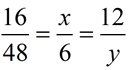The notation for ratio uses a colon, such as a : b
and is read “the ratio of a to b“. | The value of ratio a : b is expressed as the quotient of the first number, a, divided by the second number, b, where b cannot be zero. Yes, it looks like a fraction. |
Since the value of a ratio can be written as a fraction, it can also be written in any form that is equivalent to that fraction (such as a decimal or a percent).  |  | Notice that the order is important: 3 : 4 ≠ 4 : 3 because 3/4 ≠ 4/3. | 
| A unit ratio is a two-term ratio where the second term is 1. |
Example: 3 : 1 or  or 3 to 1. All ratios can be reduced to a unit ratio. or 3 to 1. All ratios can be reduced to a unit ratio. 
Consider this situation: There are 16 girls and 14 boys in a math class. Part-to-Part Comparison:
If we compare the number of girls to the number of boys, we obtain a ratio of
16 : 14 or 8 : 7
This is comparing one “part” of the class to another “part” of the class. |
| Part-to-Whole Comparison:
If we compare the number of girls to the total number of students, we obtain a ratio of 16 : 30 or 8 : 15
This is comparing one “part” of the class to the “whole” class. |
|
It is always important to read questions carefully to determine
if the ratio will be between “two parts” or between “one part and the whole”. Let’s pull these ideas together in this next example: Given:  
 | If you see a ratio such as  , it may be easier to understand what the ratio represents if you multiply both sides to remove the mixed number.  |
|
Terms used with ratios:
Continued Ratio: (the comparison for more than two quantities) a : b : c Equivalent Ratios: (all reduce to the same value 1:5) 2:10, 3:15, 1:5 or  
Visual Ways to Solve Ratio Problems: “Looking for Patterns!” |
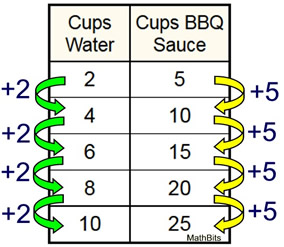
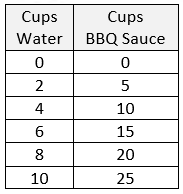
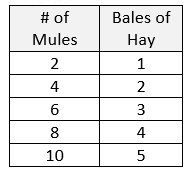
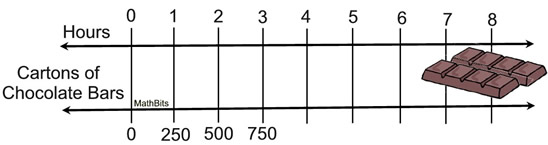
These visual representations of ratios are simply different ways to think about the same concept. They are all based on the idea that the value of a ratio can be expressed in various equivalent forms. In each situation (except for tape diagrams), we are looking to find the amount of BBQ sauce needed when using 10 cups of water. Using Ratio Table – Addition Pattern
A marinade is created with 2 cups of water and 5 cups of BBQ sauce.

Start the table with the ratio from the problem. Then add the values from this starting entry in each column. The resulting ratios are all equivalent to the starting ratio. | Using Ratio Table – Multiply Pattern 1
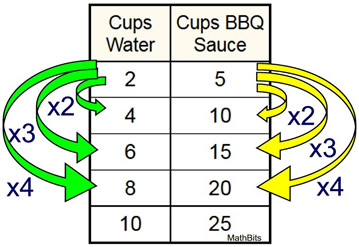
A marinade is created with 2 cups of water and 5 cups of BBQ sauce. 
To find the amount of BBQ sauce needed with 10 cups of water, just multiply 2 x 5 to get 10, and then multiply 5 x 5 to get the needed 25 cups of BBQ sauce. | Using Ratio Table – Multiply Pattern 2
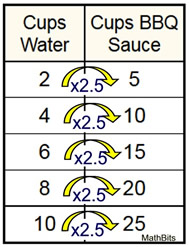
A marinade is created with 2 cups of water and 5 cups of BBQ sauce.

Once you notice the multiplication pattern you can multiply 10 cups of water by that value (2.5) to find the needed cups of BBQ sauce (25). | Using Tape Diagrams
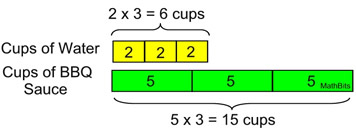
A marinade is created with 2 cups of water and 5 cups of BBQ sauce.
For this example, we are looking for the number of cups of water needed with 15 cups of BBQ sauce. 
Start by preparing boxes for the given ratio 2 : 5. Include enough BBQ boxes to get to 15. Draw in the water boxes so the number of boxes is the same as the number of BBQ boxes. Answer: 6 cups of water.
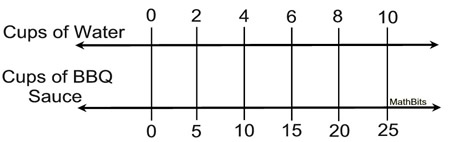
| Using Double Number Lines
A marinade is created with 2 cups of water and 5 cups of BBQ sauce.  | A double number line is set up in the same manner as setting up the addition table. Also, the addition pattern and multiplication patterns will apply to this double number line. |
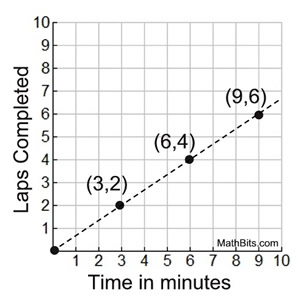
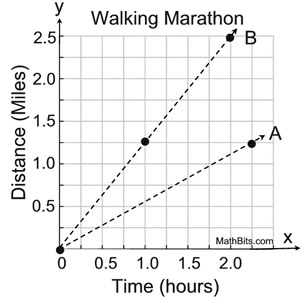
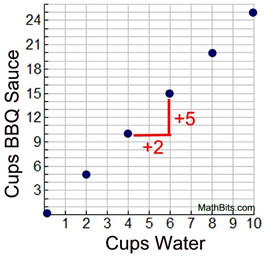
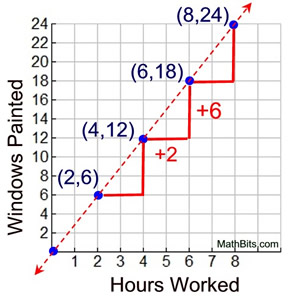
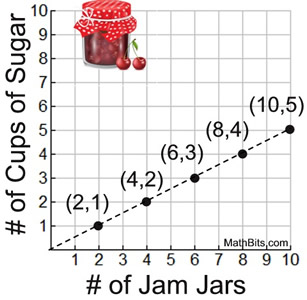
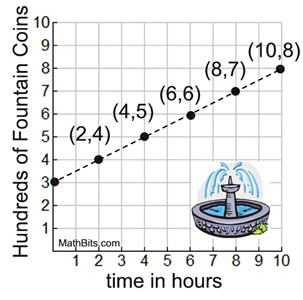
| Using a Coordinate Graph
A marinade is created with 2 cups of water and 5 cups of BBQ sauce. Preparing a table first may make it easier to prepare a graph.
The table will also clearly show that the first column will be the x-coordinates and the second column will be the y-coordinates.
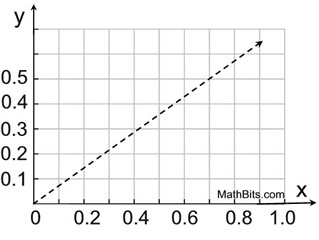
A coordinate graph will also illustrate the addition patterns and multiplication patterns seen previously.
|  The pattern across the The pattern across the
graph will show +2 to each
x-value and +5 to each y-value. |  | | Notice that the plots follow along a straight line through the origin. |
|
|

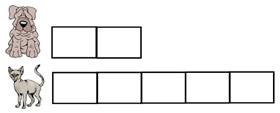
 The Callahan family has two dogs and five cats. The Callahan family has two dogs and five cats. 
Tape Diagram
Each box represents the same number of animals. | a) What is the ratio of the number of dogs to the number of cats? Answer: 2 : 5 b) What is the ratio of the number of cats to the number of dogs? Answer: 5 : 2 c) What is the ratio of the number of cats to the total number of cats and dogs? Answer: 5 : 7 |
|
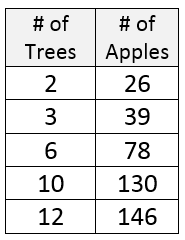
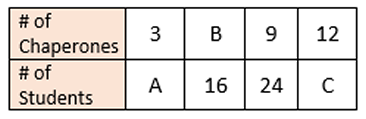
 From the chart at the right below: From the chart at the right below:a) What is the ratio of boys to girls in the class?
15 : 12 or 5 : 4 b) What is the ratio of girls to the total number of students in the class? 12 : 27 or 4 : 9 | Students in Math Class |
|
 | The table below shows possible ways a bakery can meet a specific percentage of sales of muffins.
Which of the following ratios of number of muffins sold to number of muffins baked could be included in this table? |
Choose:
1) 28 : 35
2) 24 : 40
3) 12 : 18
4) 28 : 40 | Choice 1 is correct. The ratio displayed in this table is 4 to 5 and 28 : 35 is the only choice that is equivalent to 4 : 5. |
| Specific Percentage of Sales Muffins Sold | Muffins Baked | | 8 | 10 | 16 | 20 | 20 | 25 | 32 | 40 |
|
|
 | The table below shows a constant ratio of cubic inches of water to weight of water in pounds. |
a) What is the ratio of water to weight?
The ratio is 200 : 8 or 25 : 1 b) What is the value of x?
x = 800
Since 800 : 32 is equivalent to 25 : 1.
or
Since 32 is 8 x 4, then x is 200 x 4. | Constant Ratio Water
(Cubic Inches) | Weight
(Pounds) | | 200 | 8 | 500 | 20 | x | 32 | 1500 | 60 |
|
|
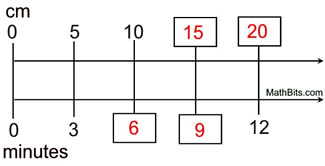
 | The double number line below shows a constant ratio of
cm : minutes to be 5 : 3. Complete the diagram. |
a) How many minutes did it take for the the distance traveled to be 10 cm.? 6 minutes b) When 12 minutes has passed, what was the distance traveled? 20 cm. c) When 9 minutes has passed, what was the distance traveled? 15 cm. | |
|
 | During the school year, a teacher graded 180 bonus quizzes. The number of quizzes receiving A’s, B’s, and C’s were in the ratio of
5 : 3 : 1, respectively. How many bonus quizzes received a grade of A for the school year? |
SOLUTION: (by Tape Diagram)
 | The tape diagram shows that 100 bonus quizzes received an A |
SOLUTION: (by Algebra)
Represent the 5 : 3 : 1 ratio
as 5x : 3x : 1x and set = to total 180
5x + 3x + x = 180
9x = 180
x = 20 |
Since the 5x represents the number of A’s, substitute 20 for x to find the final answer.
5(20) = 100
100 bonus quizzes received an A |
|

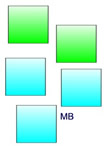
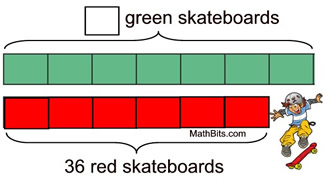
| FYI only: Ratios vs Fractions: Are the values of ratios actually “fractions”? |  | In terms of ratios, we can say:  part-to-part part-to-part
comparison2 : 3 There are 2 green boxes for every 3
blue boxes. | 
part-to-whole
comparison
2 : 5 The ratio of green
boxes to all of the
boxes is 2 to 5. |
| |
|
|
|
|
|
|
|
| | By the definition of fraction,
we can accurately say: → 2 of 5 boxes are green But the definition of fraction is not accurate for the other situation: → 2 of 3 boxes are green By definition, fractions represent parts of whole quantities. |
Conclusion: While a part-to-part comparison may be represented by a quotient, that quotient does not meet the formal definition of a fraction which is a number representing a part of a whole quantity. The part-to-whole comparison, on the other hand, does meet this definition. It is customary to see ratios (in both comparisons) written as “fractions”, which allows the ratios to be manipulated in ways similar to working with fractions.
Are the values of ratios actually fractions? Sometimes! But don’t fret the difference. |
|
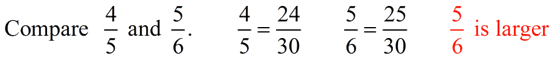
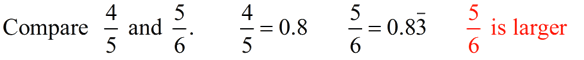
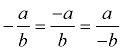
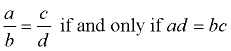
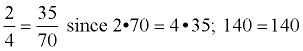
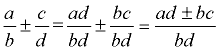
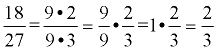
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()





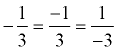
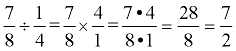
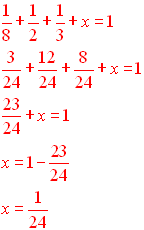

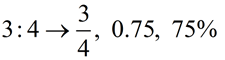


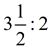 , it may be easier to understand what the ratio represents if you multiply both sides to remove the mixed number.
, it may be easier to understand what the ratio represents if you multiply both sides to remove the mixed number.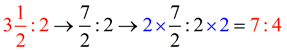
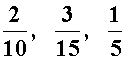




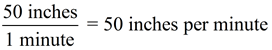

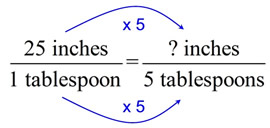
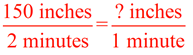
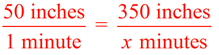
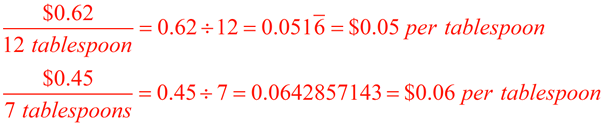
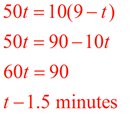
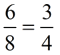

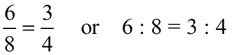
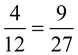
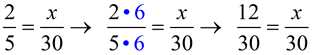

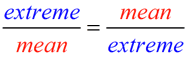
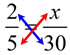
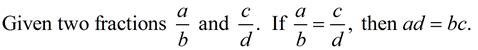
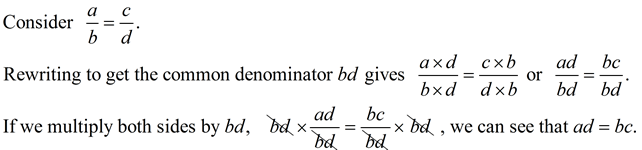
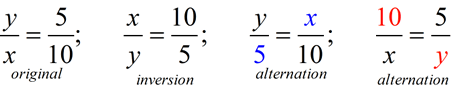

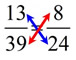
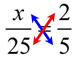

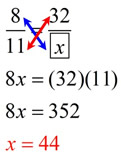
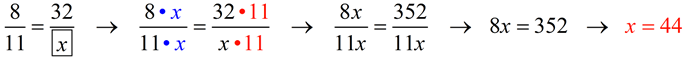
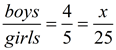
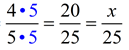
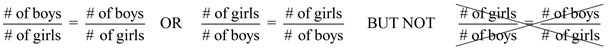
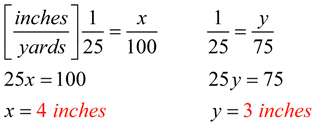


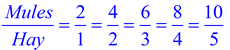
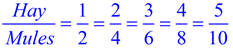

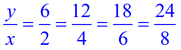
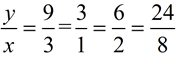
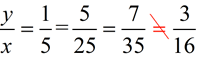
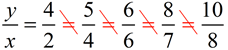

























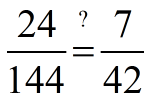 a true proportion?
a true proportion?