IB physics revision notes I’ve made for the post-2016 examinations syllabus. I got a 7 and here’s how you can too!
Important note: Please take note that although succinct notes are essential towards your revision, they should not be the only materials you cover – working through practice problems from your textbook and past papers are just as important.
Syllabus
Changes in syllabus content
Data booklet (original)
Data booklet (annotated)
Topic 1: Measurement and uncertainties
1.1 – Measurements in physics
Fundamental and derived units
Fundamental SI units
| Quantity | SI unit | Symbol |
| Mass | Kilogram | kg |
| Distance | Meter | m |
| Time | Second | s |
| Electric current | Ampere | A |
| Amount of substance | Mole | mol |
| Temperature | Kelvin | K |
Derived units are combinations of fundamental units. Some examples are:
- m/s (Unit for velocity)
- N (kg*m/s^2) (Unit for force)
- J (kg*m^2/s^2) (Unit for energy)
Scientific notation and metric multipliers
In scientific notation, values are written in the form a*10^n, where a is a number within 1 and 10 and n is any integer. Some examples are:
- The speed of light is 300000000 (m/s). In scientific notation, this is expressed as 3*10^8
- A centimeter (cm) is 1/100 of a meter (m). In scientific notation, one cm is expressed as 1*10^-2 m.
Metric multipliers
| Prefix | Abbreviation | Value |
| peta | P | 10^15 |
| tera | T | 10^12 |
| giga | G | 10^9 |
| mega | M | 10^6 |
| kilo | k | 10^3 |
| hecto | h | 10^2 |
| deca | da | 10^1 |
| deci | d | 10^-1 |
| centi | c | 10^-2 |
| milli | m | 10^-3 |
| micro | μ | 10^-6 |
| nano | n | 10^-9 |
| pico | p | 10^-12 |
| femto | f | 10^-15 |
Significant figures
For a certain value, all figures are significant, except:
- Leading zeros
- Trailing zeros if this value does not have a decimal point, for example:
- 12300 has 3 significant figures. The two trailing zeros are not significant.
- 012300 has 5 significant figures. The two leading zeros are not significant. The two trailing zeros are significant.
When multiplying or dividing numbers, the number of significant figures of the result value should not exceed the least precise value of the calculation.
The number of significant figures in any answer should be consistent with the number of significant figures of the given data in the question.
FYI
- In multiplication/division, give the answer to the lowest significant figure (S.F.).
- In addition/subtraction, give the answer to the lowest decimal place (D.P.).
Orders of magnitude
Orders of magnitude are given in powers of 10, likewise those given in the scientific notation section previously.
Orders of magnitude are used to compare the size of physical data.
| Distance | Magnitude (m) | Order of magnitude |
| Diameter of the observable universe | 10^26 | 26 |
| Diameter of the Milky Way galaxy | 10^21 | 21 |
| Diameter of the Solar System | 10^13 | 13 |
| Distance to the Sun | 10^11 | 11 |
| Radius of the Earth | 10^7 | 7 |
| Diameter of a hydrogen atom | 10^-10 | 10 |
| Diameter of a nucleus | 10^-15 | 15 |
| Diameter of a proton | 10^-15 | 15 |
| Mass | Magnitude (kg) | Order of magnitude |
| The universe | 10^53 | 53 |
| The Milky Way galaxy | 10^41 | 41 |
| The Sun | 10^30 | 30 |
| The Earth | 10^24 | 24 |
| A hydrogen atom | 10^-27 | -27 |
| An electron | 10^-30 | -30 |
| Time | Magnitude (s) | Order of magnitude |
| Age of the universe | 10^17 | 17 |
| One year | 10^7 | 7 |
| One day | 10^5 | 5 |
| An hour | 10^3 | 3 |
| Period of heartheart | 10^0 | 0 |
Estimation
Estimations are usually made to the nearest power of 10. Some examples are given in the tables in the orders of magnitude section.
1.2 – Uncertainties and errors
Random and systematic errors
| Random error | Systematic error |
| Caused by fluctuations in measurements centered around the true value (spread).
Can be reduced by averaging over repeated measurements. Not caused by bias. | Caused by fixed shifts in measurements away from the true value. Cannot be reduced by averaging over repeated measurements.
Caused by bias. |
| Examples:
Fluctuations in room temperature The noise in circuits Human error | Examples:
Equipment calibration error such as the zero offset error Incorrect method of measurement |

Absolute, fractional and percentage uncertainties
Physical measurements are sometimes expressed in the form x±Δx. For example, 10±1 would mean a range from 9 to 11 for the measurement.
| Absolute uncertainty | Δx |
| Fractional uncertainty | Δx /x |
| Percentage uncertainty | Δx/x*100% |
Calculating with uncertainties
| Addition/Subtraction | y=a±b | Δy=Δa+Δb (sum of absolute uncertainties) |
| Multiplication/Division | y=a*b or y=a/b | Δy/y=Δa/a+Δb/b (sum of fractional uncertainties) |
| Power | y=a^n | Δy/y=|n|Δa/a (|n| times fractional uncertainty) |
Error bars
Error bars are bars on graphs which indicate uncertainties. They can be horizontal or vertical with the total length of two absolute uncertainties.

Uncertainty of gradient and intercepts
Line of best fit: The straight line drawn on a graph so that the average distance between the data points and the line is minimized.
Maximum/Minimum line: The two lines with maximum possible slope and minimum possible slope given that they both pass through all the error bars.

The uncertainty in the intercepts of a straight line graph: The difference between the intercepts of the line of best fit and the maximum/minimum line.
The uncertainty in the gradient: The difference between the gradients of the line of best fit and the maximum/minimum line.
1.3 – Vectors and scalars
Vector and scalar quantities
| Scalar | Vector |
| A quantity which is defined by its magnitude only. | A quantity which is defined by both is magnitude and direction. |
| Examples:
Distance Speed Time Energy | Examples:
Displacement Velocity Acceleration Force |
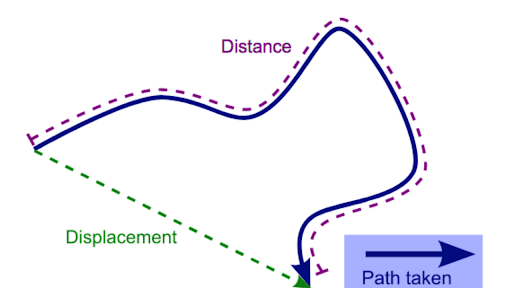
Combination and resolution of vectors
Vector addition and subtraction can be done by the parallelogram method or the head to tail method. Vectors that form a closed polygon (cycle) add up to zero.

When resolving vectors in two directions, vectors can be resolved into a pair of perpendicular components.

FYI
The relationship between two sets of data can be determined graphically.
| Relationship | Type of Graph | Slope | y-intercept |
| y=mx+c | y against x | m | c |
| y=kx^n | logy against logx | n | logk |
| y=kx^n+c with n given | y against x^n | k | c |
Topic 2: Mechanics
2.1 – Motion
Distance and displacement
| Distance | Displacement |
| Scalar | Vector |
| A scalar quantity which measures how far two locations are apart from each other along a certain path. | A vector quantity defined by the length and direction of the line segment joining the initial and final positions of an object. |

Speed and velocity
| Speed | Velocity |
| Scalar | Vector |
| Rate of change of distance to time. | Rate of change of displacement to time. |
Velocity is a measure dependent on the motion of the observer. The relative velocity of A to B is equal to the vector subtraction of the velocity of B from the velocity of A.
Acceleration
| Acceleration |
| Vector |
| Rate of change of velocity |
Acceleration due to gravity of any free-falling object is given by g=9.81m/s^2. This value does not depend on the mass of the object.
Take note that acceleration is a vector and thus has a direction. If we assume the upwards direction to be positive, the acceleration due to gravity would have a negative value of g=-9.81m/s^2.
Graphs describing motion
Displacement-time graph

The slope gradient indicates the velocity.
Straight lines imply constant velocity.
Velocity-time graph

The slope gradient indicates the acceleration.
Straight slanted lines imply constant acceleration or deceleration.
The area under the lines indicates the change in displacement.
Acceleration-time graph

Horizontal lines imply constant acceleration.
The area under the lines indicates the change in velocity.
Equations of motion for uniform acceleration
| s = displacement | u = initial velocity | v = final velocity | a = acceleration | t = time taken |
If acceleration is constant (uniform), the following equations can be used

Projectile motion
An object is said to undergo projectile motion when it follows a curved path due to the influence of gravity.


If we assume air resistance to be negligible in a projectile motion:
- The horizontal component of velocity is constant
- The vertical component of velocity accelerates downwards at 9.81m/s^2
- The projectile reaches its maximum height when its vertical velocity is zero
- The trajectory is symmetric

The presence of air resistance changes the trajectory of the projectile by the following
- The maximum height of the projectile is lower
- The range of the projectile is shorter
- The trajectory is not symmetric
Fluid resistance and terminal speed
Air resistance limits the maximum velocity an object could attain from free-falling. For example:
- If you jump out of a plane and undergo free-falling, you will feel an upward force exerted on you by the surrounding air due to air resistance.
- As you fall faster and faster due to gravity, this upward force exerted by air becomes greater and greater until it balances your weight. At this point, the net force acting on you becomes zero, and you no longer accelerate.
- This specific velocity at which you stop accelerating during a free-fall is called the terminal velocity.

2.2 – Forces
Objects as point particles
Forces change the velocity or shape of objects.
The unit of force is newton (N).
Objects are represented as a point mass to enable the representation for forces as arrows in free-body diagrams.
Free-body diagrams
On a free body diagram, forces acting on an object are represented as arrows which stem from a point mass.
The length and direction of the arrows corresponds to the magnitude and the direction of the forces acting on the body of interest.


Determining the resultant force
| 1. Resolve all acting forces into horizontal and vertical components |
| 2. Add up the horizontal components |
| 3. Add up the vertical components |
| 4. Combine the sum of horizontal components and the sum of vertical components |
Translational equilibrium
A body is said to be in translational equilibrium if it the net force acting on the body is zero. This means the body is either at rest or travels at constant velocity. For example:
- Mass hanging at rest
- Elevator moving upwards at constant velocity
- Parachutist reaching terminal velocity
Newton’s laws of motion
Newton’s First Law (Law of Inertia) states that a body remains at rest or travels with constant speed along a straight line unless acted upon by an external force. (Net force = 0)

Newton’s Second Law states that net force is directly proportional to acceleration and to mass. (F=ma)

Newton’s Third Law states that if a body A exerts a force on body B, then body B exerts a force of the same magnitude but in the opposite direction of body A.
This pair of forces is called an action-reaction pair, which must act on two different bodies.

Solid friction
Friction is a non conservative force which opposes motion. If there is no motion, then there will be no force caused by friction.
For two solid surfaces moving over each other, the friction will be affected by the nature (roughness etc) of the two surfaces. However, the surface area and velocity of the object does not affect the friction.
There are also two types of friction for solid surfaces: static friction and kinetic friction. Static friction is that which stops objects from beginning to move. Kinetic friction is that which slows objects down when they are moving. Static friction is always larger than kinetic friction.
These two types of friction are defined individually by their constants µs and µk respectively.
The forces of friction are also dependent on the normal force the surface is applying, leading to Friction force (static) =< µs * Normal force for objects that are not moving and Friction force (static) = µs * Normal force for objects that are moving.
2.3 – Work, energy and power
Kinetic energy
Kinetic energy (KE) is the energy of a body due to its motion and is given by the equation

Gravitational potential energy
The gravitational potential energy (GPE) of an object changes with its height and is given by the equation

Elastic potential energy
Elastic energy is potential energy stored as a result of the deformation of an elastic object such as the stretching of a spring and is given by the equation


Work done as energy transfer
Work done measures the transfer of energy due to a force and is a scalar quantity.
The work done W by a force F on an object is given by the equation


In a force-displacement graph, work done is the area under the curve.

Power as rate of energy transfer
Power (P) is the work done or the energy output per time given by the equation:

For constant force acting on an object with constant velocity, the power is given by the equation: P=Fv.
Principle of conservation of energy
Energy can neither be created nor destroyed; it can only be changed from one form to another. For example:
- An electrical heater transforms electrical energy to thermal energy.
- A falling object transforms potential energy to kinetic energy.
Total energy of an isolated body remains constant. In other words, ΔKE+ΔPE=0
Efficiency
Efficiency is the ratio of useful energy output to energy input as a percentage given by the equation
2.4 – Momentum and impulse
Newton’s second law expressed in terms of rate of change of momentum
The linear momentum (p) is given by the equation

The linear momentum (p) is a vector with the same direction as the velocity of an object.
The change of momentum of an object is called impulse.
Rearranging the formula describing Newton’s second law results in the following expression

Impulse and force–time graphs
Impulse is given by the area of a force-time graph.

Conservation of linear momentum
The law of conservation of linear momentum states that the sum of initial momentum is equal to the sum of final momentum in a closed system and can be given by the equation
Elastic collisions, inelastic collisions and explosions
| Type | Total momentum | Total kinetic energy |
| Elastic | Conserved | Conserved |
| Inelastic | Conserved | Not conserved |
| Explosion | Conserved | Not conserved |


Topic 3: Thermal physics
3.1 – Thermal concepts
Molecular theory of solids, liquids and gases

Molecules are held together by intermolecular forces.
The fourth state of plasma is not required to be learnt in the current syllabus.
Temperature and absolute temperature
Temperatures describe how hot or cold an object is and determines the direction of heat flow between two bodies.
Thermal energy transfers from an object with higher temperature to another object with lower temperature. The energy transfer is called heat (the flow of energy due to temperature difference). Objects which are in thermal equilibrium have the same temperature.

Temperatures in Kelvin can be calculated by deducting the temperatures in Celsius by 273.15.
![]()
The absolute temperature of a body in the Kelvin scale is directly proportional to the average kinetic energy per molecule inside the body.
Absolute zero is 0K or -273 degrees Celsius.
Temperatures cannot be lower than absolute zero. It is the temperature where particles have zero average kinetic energy (no random motion).
Internal energy
Internal energy is the sum of total kinetic energy (total thermal energy) and total potential energy.
Kinetic energy is energy associated with the random/translational rotational motions of molecules.
Potential energy is associated with forces between molecules.
Specific heat capacity
The specific heat capacity of a substance is given by

and is defined by the amount of heat needed to raise the temperature of 1kg of the substance by 1K.
Different substances have different specific heat capacities because of different densities and physical properties.
FYI
The thermal capacity of an object is given by Q=mcΔT and is defined by the amount of heat needed to raise an object’s temperature by 1K.
Phase change
| Change of phase | Process | Kinetic energy | Potential energy |
| Solid to liquid | Melting | Unchanged | Increases |
| Liquid to solid | Freezing | Unchanged | Decreases |
| Liquid to gas | Boiling | Unchanged | Increases |
| Gas to liquid | Condensation | Unchanged | Decreases |
During a phase change, temperature and kinetic energy remain constant and potential energy changes (which increases as molecules spread out and vice versa).
FYI
Boiling: Only occurs at the boiling point (a specific temperature depending on substance) and occurs throughout the liquid.
Evaporation: Can occur at any temperature and only occurs at the surface of the liquid. The fastest moving particles evaporate, decreasing the average KE of the remaining particles. As a result, temperature drops.
Specific latent heat
The specific latent heat of a substance is given by

Specific latent heat of fusion: The amount of heat required to change 1kg of a substance from solid to liquid without any change in temperature.
Specific latent heat of vaporization: The amount of heat required to change 1kg of a substance from liquid to gas without any change in temperature.

3.2 – Modelling a gas
Pressure
Pressure is defined as the normal force per unit area and is given by the equation

Equation of state for an ideal gas

where R=8.31(J/mol/K)
Kinetic model of an ideal gas
Assumptions:
- The collisions between molecules are perfectly elastic.
- The molecules are identical spheres.
- The volume of molecules is negligible compared to the volume of the gas.
- Molecules do not interact with each other except when they are in constant.
Implications:
Absolute temperature is directly proportional to the average KE and average speed of the molecules of an ideal gas.
Mole, molar mass and the Avogadro constant
Mole:
- Like the word “dozon”, a mole is a unit of quantity. It is used to measure the number of atoms or molecules.
- A mole of any material contains 6.022*10^23 atoms or molecules. The value 6.022*10^23 is called the Avogadro constant.
- The number of moles of a substance can be calculated by dividing the number of molecules of that substance by the Avogadro constant.
Molar Mass:
- The molar mass is the mass of 1 mole of any element or compound.
- Different materials/elements have different molar masses which can be found as the Mr in the periodic table.
Avogadro constant:
6.022*10^23

Differences between real and ideal gases
The ideal gas is based on a list of assumptions stated previously. However, in real gases, such assumptions may not be true.
- Forces exist between gas molecules in real gases (intermolecular forces).
- The volume of molecules is not negligible compared to the volume of gas in real gases.
Real gases may behave similarly to ideal gases under high temperatures and low pressure.
Topic 4: Waves
4.1 – Oscillations
Simple harmonic oscillations
Oscillations are periodic motions which center around an equilibrium position.
Simple harmonic motion (SHM) is a special type of oscillation. For example:
- The simple pendulum
- The vibration of strings in a violin
- The spring-mass system, where the mass is initially displaced to produce a periodic motion around the equilibrium position
An object undergoes SHM if it experiences a force which is proportional and opposite of the displacement from its equilibrium position.
The period is independent of the amplitude of the SHM and can be given by the following equation
for a pendulum
and

for a spring-mass system
Time period, frequency, amplitude, displacement and phase difference
| Displacement (x) | Amplitude | Period (T) | Frequency (f) | Phase difference |
| Displacement of the oscillating object at a specific time from its equilibrium position | Maximum displacement of the oscillating object | Time taken for one complete oscillation (in seconds) | Number of times the object oscillates per unit time (usually one second)
f=1/T | The difference between two SHMs with the same frequency in terms of their relative position in a cycle measured in radian |

Conditions for simple harmonic motion
- When the body is displaced from equilibrium, there must exist a restoring force (a force that wants to pull the body back to equilibrium).
- The magnitude of the restoring force must be proportional to the displacement of the body and acts towards the equilibrium.
4.2 – Travelling waves
Travelling waves
A travelling wave is a continuous disturbance in a medium characterized by repeating oscillations. For example:
- A rope that is flicked up and down continuously creates a repeating disturbance similar to the shape of a sine/cosine wave.
Energy is transferred by waves.
Matter is not transferred by waves.
The direction of a wave is defined by the direction of the energy transfer.
Wavelength, frequency, period and wave speed

Wavelength, frequency, and period follow the same rules of SHM.
Wave speed can be calculated by the following equation

Transverse and longitudinal waves
| Transverse wave | Longitudinal wave |
The direction of oscillation is perpendicular to the direction of the wave
| The direction of oscillation is parallel to the direction of the wave |
| Example:
Water waves Wave in a string flicked up and down Light (electromagnetic waves) | Example:
Wave produced in a spring Sound waves Earthquake P-waves |
FYI
| Transverse wave | Longitudinal wave |
| A point with maximum positive displacement is called a crest.
A point with minimum displacement is called a trough. | A region where particles are closed to each other is called a compression.
A region where particles are furthest apart from each other is called a rarefaction. |
 |  |
The nature of electromagnetic waves
All EM waves travel in vacuum at the same speed of 3*10^8m/s.
EM waves are transverse waves.

The nature of sound waves
The speed of sound in 20 degrees Celsius dry air is approximately 343.2m/s.
Sound waves are longitudinal waves.

4.3 – Wave characteristics
Wavefronts and rays
Wavefronts:
- Lines joining points which vibrate in phase.
- Can be straight lines or curves.
- The distance between successive wavefronts is the wavelength of the wave.
Rays:
- Lines which indicate the direction of wave propagation.
- Rays are perpendicular to wavefronts.

Amplitude and intensity
The amplitude and intensity of a wave depends on its energy.
The intensity of a wave is proportional to the square of its amplitude (I∝A^2).

Transverse and longitudinal waves
See previous section with the same title.
Superposition
The principle of superposition states that the net displacement of the underlying medium for a wave is equal to the sum of the individual wave displacements.

The left shows constructive interference (superposition) where the two waves add up (e.g. 1+1=2). The right shows deconstructive interference (superposition) where the two waves cancel each other (e.g. 1+(-1)=0).
Polarization
Light is a transverse wave (polarization only occur to transverse waves).
The polarization of light refers to the orientation of the oscillation in the underlying electric field.
Light is plane polarized if the electric field oscillates in one plane.

Left shows unpolarized light and right shows polarized light.
Polarization by reflection
When light is transmitted across a boundary between two mediums with different refractive indexes, part of the light is reflected and the remaining part is refracted (for further explanation, see section 4.4).
The light reflected is partially polarized, meaning that it is a mixture of polarized light and unpolarized light.
The extent to which the reflected light is polarized depends on the angle of incidence and the refractive index of the two mediums.
The angle of incidence at which the reflected light is totally polarized is called the Brewster’s angle (ϕ) given by the equation

where n1 and n2 are the refractive indexes for their respective mediums
When the angle of incidence is equal to Brewster’s angle, the reflected ray is totally polarized and the reflected ray is perpendicular to the refracted ray.

Polarizers and Analyzers
Polarizer:
- A polarizer is a sheet of material which polarizes light.
- When unpolarized light passes through a polarizer, its intensity is reduced by 50%.
Analyzer:
- When polarized light passes through a polarizer, its intensity will be reduced by a factor dependent on the orientation of the polarizer. This property allows us to deduce the polarization of light by using a polarizer.
- A polarizer used for this purpose is called an analyzer.
Malus’ Law relates the incident intensity and transmitted intensity of light passing through a polarizer and an analyzer.

where I is the transmitted intensity, I0 is the initial light intensity upon the analyzer, θ is the angle between the transmission axis and the analyzer.

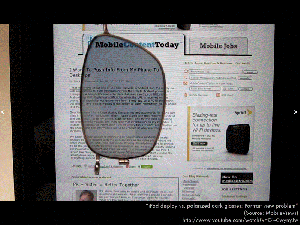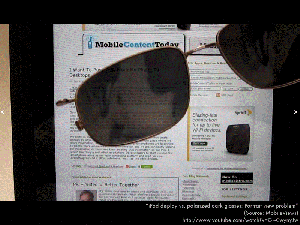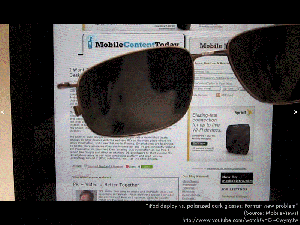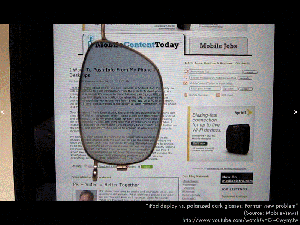
When light passes through an optically active substance, the plane of polarization rotates.
4.4 – Wave behaviour
Reflection and refraction
Reflection

Angle of incidence = Angle of reflection
Reflection of waves from a fixed end is inverted.

Reflection of waves from a free end is not inverted.

Refraction
Refraction is the change in direction of a wave when it transmits from one medium to another.

The angle of incidence and the angle of refraction can be determined by Snell’s law given by the following formula

where n1 and n2 are the refractive indexes for their respective mediums


Fast-to-slow: towards normal; slow-to-fast: away from normal
In addition, the refractive index n1 and n2 are related by the following equation

where v1 and v2 are the speed of the waves in their respective mediums and λ1 and λ2 are the wavelength of the waves of their respective mediums

Snell’s law, critical angle and total internal reflection
See previous section (Reflection and refraction) for Snell’s law.

The refractive index and the critical angle are related by the following equation Total internal reflection only occurs when the light ray propagates from a optically denser medium to an optically less dense medium.
Total internal reflection only occurs when the light ray propagates from a optically denser medium to an optically less dense medium.
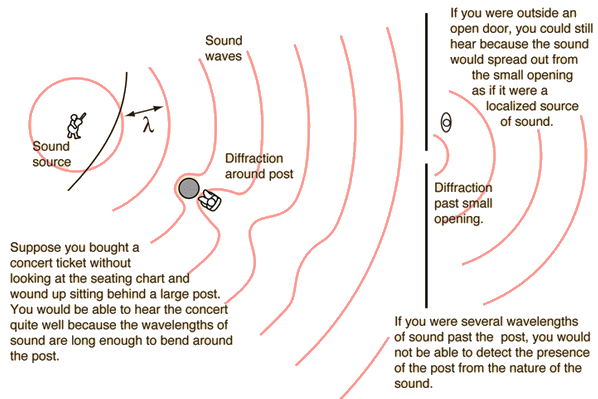
Diffraction through a single-slit and around objects
- Diffraction through a single-slit

Single-slit equations are not required for the standard level course.
- Diffraction around objects
Interference patterns
Maximums form at constructive interference (the maximum is shown by 1-2) and minimums form at deconstructive interference (the first minimum is shown by 3-4).




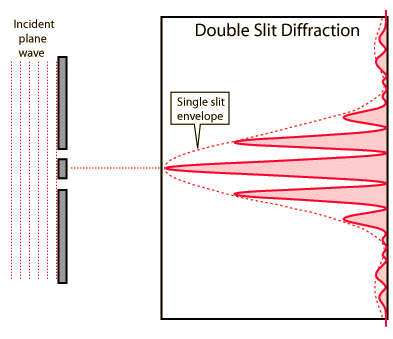
Double-slit interference
Like single-slit diffraction, double-slit diffraction occurs via the same methods of interference and has a similar diffraction pattern.

Path difference



4.5 – Standing waves
The nature of standing waves
Standing waves (stationary) waves result from the superposition of two opposite waves which are otherwise identical.
Energy is not transferred by standing waves.

A wave hits a wall and is reflected identically opposite.

The black wave shows the wave created by the superposition of the blue and green waves.

Boundary conditions
Air particles can oscillate and create standing waves in pipes with open or closed ends.
Antinodes are positioned at open ends and nodes are positioned at closed ends.
Standing waves on a string is equivalent to that in a pipe which is closed on both ends (nodes-node).

The following table summarizes the behavior of standing waves in pipes and strings:
| One closed end and one open end | Two closed ends | Two open ends |
 | 1st Harmonic
|  |
 | 2nd Harmonic
|  |
 | 3rd Harmonic
|  |
| nth Harmonic
λ=4L/n (Note that even harmonics do not exist for pipes with one closed end and one open end) | nth Harmonic
λ=2L/n | nth Harmonic
λ=2L/n |
Nodes and antinodes
Positions along the wave which are fixed are called nodes (minimum) and those with the largest displacement are called antinodes (maximum).
For standing waves, the distance between adjacent nodes = the distance between adjacent antinodes = λ/2.

FYI
Difference between standing waves and travelling waves
| Standing waves | Travelling waves |
| No energy is propagated along a standing wave
A standing wave has nodes and antinodes The amplitude of the standing wave varies along the wave Particles between two adjacent nodes oscillate in phase and particles separated by exactly one node oscillate in antiphase. | Energy is propagated in a travelling wave
A travelling wave has neither nodes nor antinodes The amplitude of the travelling wave is constant throughout the wave The phase difference between two particles of a travelling wave can take any value between 0 and 2π |
Topic 5: Electricity and magnetism
5.1 – Electric fields
Charge
Electric charge can either be positive or negative.
Charges with the same sign repel each other and changes with the opposite sign attract.

An object with equal amounts of positive change and negative charge is said to be electrically neutral.
The unit of electric charge is coulomb (C).
The charge of one electron is equal to 1.6*10^-19C.
Electric charge is always conserved. While charges could migrate from one body to another, the total charge remains the same.
FYI
Conductors are materials which allow the passage of electric charge. This is due to the presence of free electrons in solid conductors.
- Examples of conductors include all metals, graphite, humans.
Insulators are materials which do not allow the passage of electric charge.
- Examples of insulators include wood, glass, and plastic buckets.

Electric field
Electric fields can be graphically represented as electric field lines.
- The direction of the field at a point is equal to the direction of the field line passing through that point (arrows from the positive pole to the negative pole).
- The magnitude of the field at a point corresponds to the density of the field lines around that point. For a uniform electric field, the field lines are straight, parallel and equally spaced.
Non-uniform electric field

Uniform electric field

The electric field lines curve outwards near the edge of the plates. This is known as the “edge effect”.
Electric field strength (E) is the force per unit charge experienced by a positive test change placed in a field.
Coulomb’s law states

where F is the force, q1 and q2 are the charge of the two objects (usually the same when considering two electrons), and r is the radius/distance between the two charges.
Therefore, since F = qE = kqq/r^2, we can deduce that for non-uniform electric fields, the electric field strength can be calculated by

by cancelling out q (charge) on both sides.
For uniform electric fields, the electric field strength can be calculated by
Coulomb’s law
See previous section (Electric field).
Electric current
The existence of an electric potential difference (see the last section of 5.1) across an object causes charges to flow through the object.
Electric current (I) refers to the rate of flow of electric charge and can be given by the equation

The direction of an (conventional) electric current is opposite to the direction of electron flow.

Direct current (dc)
Direct current (dc) is a uniform current flowing in one fixed direction in a circuit.
Direct current is usually supplied by acid-based batteries or dry cells.

Potential difference
The electric potential difference (pd) between two points is equal to the work done (energy) required per unit charge to move from one point to another. It is also known as voltage (V).

Voltage is analogical to the differences of upstreams and downstreams where water flow in the stream is the flow of electrons within the circuit.

5.2 – Heating effect of electric currents
Circuit diagrams
An electric circuit is an interconnection of electrical components in a closed loop.

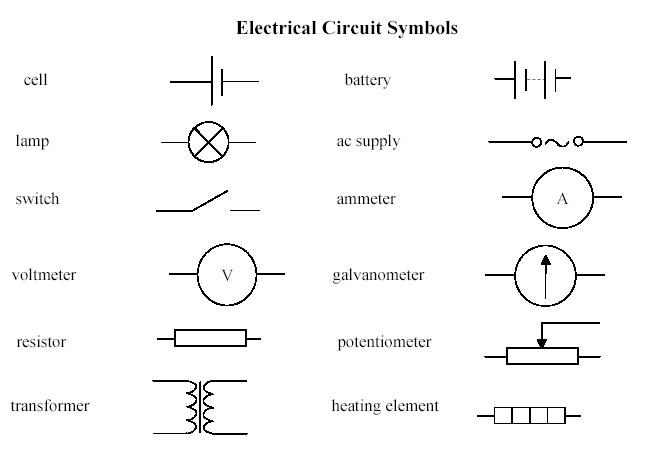
Resistors
A resistor is an electrical component which implements a specific resistance within an electric circuit.
A resistor with adjustable resistance is called a variable resistor.
Resistors can be connected in series or in parallel.

FYI

Voltmeters
A voltmeter is used to measure the potential difference between two points.
A voltmeter should be connected in parallel with the components being measured.
An ideal voltmeter has infinite resistance.
Ammeter
An ammeter is used to measure the current passing through a point.
An ammeter should be connected in series at the point of measurement.
An ideal ammeter has zero resistance.

Kirchhoff’s circuit laws
Kirchhoff’s junction rule is a statement of the conservation of charge flow per time. The sum of all currents flowing into a junction must equal the sum of all currents flowing out.

Kirchhoff’s loop rule is a statement of the conservation of electric potential energy per charge. For a complete loop of an electrical circuit all of the electric potential rises added together must equal all of the electric potential drops added together.

Resistance expressed as R=V/I
The resistance (R) of an object can be seen as a measure of opposition to electric current through the object.
It is given by the ratio between the electric potential difference (V) and the current induced (I).

Ohm’s law
Ohm’s law states that the current flowing through a conductor is proportional to the electric potential difference across the conductor.
- If we plot current versus potential difference, the slope of the resulting graph is constant.
Ohm’s law is not always obeyed. A conductor which obeys Ohm’s law has a constant resistance and is called an Ohmic conductor.
A non-ohmic conductor portrays a graph that does not have a constant gradient (non-linear).

Resistivity
The resistance of an object is proportional to its length (L) and inversely proportional to its cross-sectional area (A).
The resistance is influenced by the resistivity constant of the object (determined by the material it is made out of).

Power dissipation
The power (P) dissipated in a resistor can be given by

FYI

This means electrical energy is “lost” as heat energy or other forms of energy that are not considered useful over time.

5.3 – Electric cells
Cells
A cell in a circuit acts as a source of electrical energy and creates an electric potential difference at its terminals.
A battery is made up of two cells connected.

Internal resistance
The internal resistance is the resistance of a source determined by the material it is made up of.
The internal resistance can be used to calculated the emf. (see the last section of 5.3)
Secondary cells
A secondary cell or battery can be recharged after use by passing current through the circuit in opposite direction to the current during the discharge.

Terminal potential difference
The potential difference at the terminals of a source is less than the emf of the source due to internal resistance. (see the last section of 5.3)
Electromotive force (emf)
The electromotive force (emf) of a source is defined as the energy per unit charge supplied by the source.
The unit for emf is volt (V).


5.4 – Magnetic effects of electric currents
Magnetic fields
Magnetic fields are caused by the presence of magnets or moving charges.
Similar to how an electric charge experiences a force in an electric field, a magnet or an electric current experiences a force in a magnetic field.
The unit of a magnetic field is Tesla (T).

Magnetic field patterns
Magnetic fields can be graphically represented using magnetic field lines.
- The direction of the field at a point is equal to the direction of the field line passing through that point.
- The magnitude of the field at a point corresponds to the density of the field lines around that point.
Magnets

Wire with current

Solenoid with current

FYI
Viewing the magnetic field in 3D, dots represent magnetic fields coming out of the page (like the tip of an arrow) and crosses represent magnetic fields going into the page (like the nock of an arrow).

Magnetic force
The magnitude of the force acting on a current-carrying wire due to a magnetic field can be given by

The equation may be multiplied by sinθ where θ is the angle between the direction of the field and the current. This can be ignored when θ=90 degrees because sin90 degrees equals to 1.
Magnetic force on a moving charge
The magnitude of the force acting on a moving charge due to a magnetic field can be given by

where F is the force acting on the wire, B is the magnetic field, q is the amount of charge, v is the velocity of the charge, and θ is the angle between the direction of the field and the velocity.

Remember that the direction of the (conventional) current is the opposite to that of the flow of electrons.
As the magnetic force is always perpendicular to the velocity of the charge, it acts as a centripetal force (see topic 6) and the charge follows a circular path. No work is done on the charge by the magnetic field.


Topic 6: Circular motion and gravitation
6.1 – Circular motion
Period, frequency, angular displacement and angular velocity
Uniform circular motion refers to circular motion at constant speed.
In a uniform circular motion, speed is constant while (angular) velocity and (angular) acceleration are constantly changing.
- While the magnitude of its velocity remains constant, the direction of its velocity is constantly changing.
- The acceleration causing this change in velocity is always directed towards the center of the circular path.

The period is the time taken for the object to complete one full circle and is usually calculated in seconds. The frequency can be calculated by 1/period and is usually measured in Hz.
Centripetal force
Centripetal force is the corresponding force (resultant force) which causes the centripetal acceleration.
Properties:
- Direction: Pointing towards the center of the circle / perpendicular to the instantaneous velocity
- Magnitude:

- Work done by centripetal force = 0
- Centripetal force is not a type of force; rather, it is just the name we give to the net force causing a circular motion. For example:



Centripetal acceleration
The acceleration which gives rise to a circular motion is called the centripetal acceleration. Its magnitude is given by

It is directed towards the center of the circular motion and is perpendicular to the instantaneous velocity of the object.
6.2 – Newton’s law of gravitation
Newton’s law of gravitation
The gravitational force between two objects can be calculated using Newton’s universal law of gravitation


Gravitational field strength
The gravitational field strength at a point is the force per unit mass experienced by a test mass at that point.
The gravitational field strength (g) due to an object is given by

Gravitational field strength at the surface of a planet
- The gravitational field strength at the surface of a planet can be calculated by using the equation for gravitational field strength and substituting M and r by the mass and the radius of the planet respectively.
- If we calculate the gravitational field strength at the surface of the Each using the mass and the radius of the Earth, we would obtain the value 9.81m/s^2, which is equal to the acceleration due to gravity on the surface of the Earth.
- Different planets have different radii and masses. Consequently, different planets have different gravitational field strengths.
Topic 7: Atomic, nuclear and particle physics
7.1 – Discrete energy and radioactivity
Discrete energy and discrete energy levels
- The electrons of an atom can occupy certain discrete atomic energy levels.
- As an electron makes a jump from one energy level to another, energy is absorbed or released in the form of a photon. The amount of energy absorbed or released is equal to the difference between the discrete atomic energy levels and is also quantized.
- The energy of a photon is dependent on its frequency. Therefore, only photons with frequencies which correspond to the differences between the atomic energy levels can be absorbed or released by an atom. These frequencies appear as spectral lines in the emission and absorption spectra.

- The existence of discrete energy levels called atomic energy levels can be supported by the emission spectra and the absorption spectra of atoms.

Transitions between energy levels
When the electrons within an atom jump from one atomic energy level to a lower energy level, energy is released in the form of light. Likewise, light is absorbed when the electrons within an atom jump from one atomic energy level to a higher energy level.

The amount of energy absorbed or released can be calculated by the difference in energy (eV) between the two energy levels.
Radioactive decay
- Radioactive decay refers to the spontaneous random process by which particles or electromagnetic radiation is emitted from an unstable nucleus. The product nucleus from a radioactive decay is called a daughter nucleus.
- The daughter nucleus is energetically unstable.
- The activity of radioactive decay can be shown by half-lives.

- The radioactive half-life of a substance is the time it takes for half of its radioactive nuclei to decay.
- If we plot the amount of radioactive nuclei which have not yet decayed with time, the resulting curve is called the decay curve and can be shown as the following.

Fundamental forces and their properties




Alpha particles, beta particles and gamma rays
Alpha particles
 An alpha particle is a helium nucleus.
An alpha particle is a helium nucleus.
- It has a relative charge of +2.
- Its penetration power is the lowest among the three types of particles and can be blocked by a piece of paper or a few cm of air.
- Its ionizing power is the highest among the three types of particles.
Beta particles

 A beta particle is an electron or a positron.
A beta particle is an electron or a positron.
- It has a relative charge of -1 or +1.
- Its penetration power is in the middle among the three types of particles and can be blocked by a thin sheet of aluminum.
- Its ionizing power is in the middle among the three types of particles.
Gamma rays

- Gamma rays are photons.
- It does not have a charge.
- Its penetration power is the highest among the three types of particles and can be blocked by several cm of lead.
- Its ionizing power is in the lowest among the three types of particles.


Half-life
See previous section (Radioactive decay).
Absorption characteristics of decay particles
| Short-term effects | Long-term effects |
| Radiation burn
Nausea and vomiting Diarrhea Headache | Cancer
Genetic mutations |
Isotopes

Different isotopes of a given element have the same atomic number (atomic number defines the type of element) but different mass numbers because they have different numbers of neutrons.
Background radiation
Background radiation comes from natural sources and artificial sources.
- Natural sources: cosmic rays from space, radioactive rocks and soil, living organisms that have consumed radioactive substances in the food chain
- Artificial sources: radioactive waste from nuclear power plants, radioactive fallout from nuclear weapons, medical x-rays
Average composition and exposure of background radiation


7.2 – Nuclear reactions
The unified atomic mass unit
The unified atomic mass unit (μ) is commonly used in nuclear physics. It is defined as one twelfth of the mass of a carbon-12 atom.

Mass defect and nuclear binding energy
Mass defect
- The difference between the mass of an atom and the sum of mass of its constituent parts is called its mass defect.
- Mass defect can be explained by Einstein’s mass-energy equivalence: As energy required to break apart a nucleus, the sum of energy contained in the constituent nucleons is higher than that of the combined nucleus. Energy is related to mass.
Nuclear binding energy
- The nuclear binding energy of a nucleus is the amount of work required to separate the nucleons inside the nucleus.
- Binding energy per nucleon = binding energy of nucleus / number of nucleons in nucleus.

where E is energy in J, m is mass in kg, and c is the speed of light in m/s
FYI
The nuclear binding energy curve

Nuclear fission and nuclear fusion
Nuclear fission
- Nuclear fission is the splitting of a heavy nucleus into two lighter nuclei.
- A great amount of energy is released in nuclear fission due to the greater binding energy of the daughter nuclei.
- Nuclear fission is used in nuclear power plants.
Nuclear fusion
- Nuclear fusion is the joining of two light nuclei to form a heavy nucleus.
- A great amount of energy is released in nuclear fusion due to the greater binding energy of the daughter nucleus.
- Nuclear fusion yields more energy than nuclear fission.
- Nuclear fusion is the main source of the sun’s energy.

7.3 – The structure of matter
Quarks, leptons and their antiparticles
- Quarks and leptons are the elementary particles (building blocks) of matter.
- Each particle also has an antimatter counterpart.
- When matter collides with its corresponding antimatter, the particles annihilate and release energy by mass-energy equivalence.

Hadrons, baryons and mesons

- As stated in the previous section, the elementary particles of matter comprises of quarks and leptons.
- Hadrons are made up of quarks and are identified in the same classification level as leptons.
- Unlike leptons, which do not experience the strong nuclear force, hadrons experience all four fundamental forces.
- Hadrons are generally larger than leptons.
- Hadrons are sub-divided into baryons and mesons.
- Baryons and mesons are made up of different types of quarks and antiquarks.


where u represents up quarks, d represents down quarks, c represents charm quarks, s represents strange quarks, (t represents top quarks), b represents bottom quarks, and the line above the representative letter of the quarks indicate its corresponding antiquarks.
- The conservation laws of charge, baryon number, lepton number and strangeness
- When writing equations, we already know that the charge of the reactants and the products must be identical due to the conservation law of charge.
- In particle physics, other than the conservation of charge, the baryon number, lepton number, and strangeness must also be conserved.
- Baryons have a baryon number of +1, antibaryons have a baryon number of -1, leptons have a lepton number of +1, and antileptons have a lepton number of -1.
- The conservation of strangeness (strange quark) only occurs within interactions of the strong nuclear force while the conservation of the other three properties apply to all interactions.
The nature and range of the strong nuclear force, weak nuclear force and electromagnetic force
See previous section in 7.2 (Fundamental forces and their properties).
Exchange particles
Exchange particles of the four fundamental forces are gluons, photons, W+ bosons, W- bosons, Z0 bosons, and gravitons.

See previous section in 7.2 (Fundamental forces and their properties).
Feynman diagrams
- Feynman diagrams, introduced by physicist Richard Feynman, can be used to express the behavior of subatomic particles over time.
- Feynman diagrams are read from the left to the right where the x-axis shows time and the y-axis shows roughly the space direction of the subatomic particle interactions. Some Feynman diagrams, such as the examples given below, switch the x-axis and the y-axis where the progression of the interactions with time is read upwards.

Some examples of Feynman diagrams


For a comprehensive guide on how to draw Feynman diagrams, visit http://www.quantumdiaries.org/2010/02/14/lets-draw-feynman-diagams/.
Confinement
Quarks and gluons (massless subatomic particles that transmit the force binding quarks together in a hadron) are color-charged particles. Similar to electrically-charged particles which interact by exchanging photons in electromagnetic interactions, color-charged particles exchange gluons in strong force interactions. Note that color charge has nothing to do with visible colors. It is just an expression.
When two quarks are close to each other, they exchange gluons and create a strong color force field that binds quarks together. The force field gets stronger as the quarks get further apart. Quarks constantly change their color charges as they exchange gluons with other quarks. There are 3 color charges and 3 corresponding anti-color charges.

Just as mixing red, blue, and green visible colors yield white, mixing red, blue, and green color charges yield color neutral.
Color confinement is a phenomenon that color-charged particles cannot be isolated singularly and therefore cannot be directly observed. The color-charged quarks are said to be confined in groups (hadrons) with other quarks which composite to color neutral and cannot be distinguished separately. This is because the color force increases as the color-charged quarks are pulled apart.
TL;DR: Color confinement or quark confinement is the phenomenon when isolated quarks and gluons cannot be observed.
The Higgs boson
In addition to the three generations of leptons and quarks (see previous section (Quarks, leptons and their antiparticles)), there are four classes of bosons and an additional highly massive boson called the Higgs boson. This particle was proposed in 1964 to explain the process which particles can acquire mass and was identified with the Large Hadron Collider (LHC).

FYI
The Large Hadron Collider (LHC) is the world’s largest and most powerful particle collider, the largest and most complex experimental facility ever built, and the largest single machine in the world. It was built by CERN in collaboration with over 10000 scientists and engineers from over 100 countries along with hundreds of universities and laboratories.

Our changing views of the atom model

Summary of fundamental particles and interactions

Topic 8: Energy production
8.1 – Energy sources
Specific energy and energy density of fuel sources
- Specific energy and energy density are useful measures of the energy that will be released from a given weight or volume of fuel when it is burned.
- Specific energy is the energy per unit mass of the fuel and can be given by energy/mass
- Energy density is the energy per unit volume of a fuel and can be given by energy/volume.
Sankey diagrams
Energy degradation
- While energy may be completely converted into work in a single process, a cyclical process is required to convert thermal energy to work continuously.
- In accordance with the second law of thermodynamics, some energy will be lost to the surroundings and cannot be used to perform useful work. The unavailable energy is called degraded energy.
Sankey diagram
- A Sankey diagram is a type of energy diagram where the width of each arrow is proportional to the amount of energy in that section.


Primary energy sources
Primary energy sources are found in nature and have not been subjected to any conversion or transformation process.


Electricity as a secondary and versatile form of energy
Electricity is a secondary and versatile form of energy.
Production of electrical power:
- Fuel is used to boil water to produce pressurized steam.
- The pressurized steam drives a turbine which is connected to coils of wire.
- When the turbine rotates, the coils of wire move through a strong magnetic field. Electrical power is produced via electromagnetic induction in the generator.

- Renewable and non-renewable energy sources
- There are two categories of primary energy sources: renewable energy resources and non-renewable energy resources.
- Renewable energy sources are the ones which cannot be depleted.
- Non-renewable energy sources can be used up and become depleted.
- Most energy sources derive their energy from the sun directly (e.g. solar power) or indirectly (e.g. fossil fuels).
| Renewable energy sources | Non-renewable energy sources |
| Solar power
Wind power Hydroelectric power Tidal power Geothermal Biomass | Coal
Oil Natural gas Nuclear power |
8.2 – Thermal energy transfer
Conduction, convection and thermal radiation

Conduction and convection requires a transmittance medium while radiation does not and can be transferred through a vacuum (e.g. outer space).
Black-body radiation
- A black body which absorbs all incident electromagnetic radiation is both the perfect absorber and the perfect emitter of radiation.
- The radiation emitted by such a body at constant temperature is called black-body radiation.
- The Stefan-Boltzmann law states that the power of radiation emitted by a black body per unit area is proportional to the fourth power of its temperature.

Emission spectrum of a black body

Albedo and emissivity
Albedo
- The Albedo (α) of a planet is defined as the ratio between the total scattered (reflected) radiation and the total incident radiation of that planet.
- Albedo = total scattered power / total incident power
- The albedo of a planet is affected by the following:
- Season (cloud formations)
- Latitude
- Terrain (ocean has low albedo because it mainly absorbs and snow has high albedo because it mainly reflects)
- The global annual mean albedo is about 0.3 (30%) on Earth.
Emissivity
- Most objects are not black bodies. They radiate a fraction of the power per unit area compared to a black body at the same temperature. The value of this fraction depends on the object and is called the object’s emissivity (e).
- Emissivity = power per unit area radiated by the object / power per unit area radiated by a black body at the same temperature.
- The equation for the power radiated by an object with emissivity e can be given by the diagram in the previous section (Black-body radiation).
- The solar constant
- The solar constant is the amount of energy that normally falls on a unit area (1m^2) of the Earth’s atmosphere per second when the Earth is at its mean distance from the sun.
- The solar constant is approximately 1366 W/m^2.

The greenhouse effect
Greenhouse gases:
- Greenhouse gases absorb infrared radiation because its molecules have natural frequencies in the infrared region and readily absorb infrared radiation due to resonance.

Mechanism:
- Incoming radiation from the sun takes form of ultraviolet and visible radiation.
- Some of this radiation is absorbed by the Earth’s atmosphere and some of the radiation is reflected back into space by the Earth’s surface (ground).
- The radiation which is reflected back into space takes form of infrared radiation.
- The greenhouse gases present in the atmosphere absorb infrared radiation and reflect it back towards the Earth’s surface.
- Thus, heat energy becomes trapped inside Earth’s atmosphere and accumulates, leading to the greenhouse effect and an increase in average mean temperatures on Earth.
Chain reaction:
- Global warming reduces ice/snow cover. This causes a decrease in albedo and increases the rate of heat absorption by the Earth.
- The solubility of carbon dioxide in the sea decreases with increasing temperature, leading to an increase in atmosphere carbon dioxide (greenhouse gas) concentration.
Effects:
- Rise in mean sea level by the melting of ice on land.
- Extreme weather such as heat waves and heavy floods.

Energy balance in the Earth surface–atmosphere system
Earth’s energy balance describes how the incoming energy from the sun is used and returned to space. If incoming and outgoing energy are in balance, the Earth’s temperature remains constant.

Topic 9: Wave phenomena (HL)
9.1 – Simple harmonic motion
The defining equation of SHM
By Newton’s Second Law, SHM can be defined as the following equations

where x0 is the amplitude (maximum displacement), x is the displacement, v is the velocity, and a is the acceleration.
The angular frequency ( w ) is related to the period of the SHM by the following equation

Energy changes
In a SHM, there is an interchange between KE and PE throughout the motion. However, the total energy remains constant.

Summary:
- At maximum displacement, PE is at max while KE=0
- At zero displacement, KE is at max while PE=0
- At minimum displacement, PE is at max while KE=0
- Total energy (KE+PE) remains constant throughout the motion

9.2 – Single-slit diffraction
The nature of single-slit diffraction
Special diffraction patterns appear when light is diffracted by a single slit which is comparable to the wavelength of the light in size.
We can represent this diffraction pattern by plotting the light intensity against the angle of diffraction.
The angle of diffraction for the first minimum θ can be given by

where λ is the wavelength and a is the size/length of the slit

![]()
where λ is the wavelength, m is the order of the maximum, D is the distance of the slits to the screen, and a is width of the slit.
9.3 – Interference
Young’s double-slit experiment


where λ is the wavelength, m is the order of the maximum, D is the distance of the slits to the screen, and d is the distance between the two slits.
Modulation of two-slit interference pattern by one-slit diffraction effect
The previously section shows an ideal double-slit which ignores the single-slit characteristics of each of the two single-slits. A true double-slit would exhibit closely spaced dark and light areas (fringes) superimposed over the single-slit pattern. The single-slit profile is said to modulate the double-slit pattern.

Multiple slit and diffraction grating interference patterns
- Multiple slit interference patterns


- Diffraction grating interference patterns
A diffraction grating is the tool of choice for separating the colors in incident light.
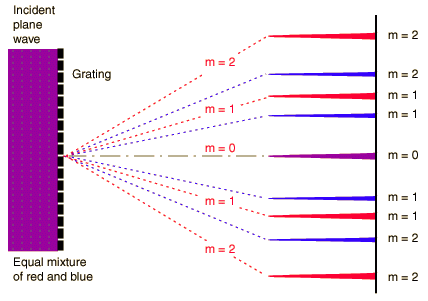
The condition for maximum intensity is the same as that for a double-slit. However, the angular separation of the maxima is generally much greater because the slit spacing is so small for a diffraction grating.
The equation

is the condition for angles at which constructive interference occurs (maximum) where d is the distance between gratings and m is the order of the maximum.

Thin film interference
Interference between light waves is the reason that thin films, such as soap bubbles, show colorful patterns.
The interference of light waves reflects off the top surface of a film with the waves reflecting from the bottom of the surface.

![]()

9.4 – Resolution
The size of a diffracting aperture
When light from a point source passes through a small circular aperture, it does not produce a bright dot as an image, but rather as a diffused circular disc.

The greater the diameter of the diffracting aperture (such as the diameter of the pupil in the human eye or the diameter of the lens in a telescope), the better resolved (clearer) the image is.
The resolution of simple monochromatic two-source systems
Consider the diffraction pattern of two light beams diffracted by a single slit. These patterns can be categorized as resolved, just resolved, or not resolved depending on the separation between the images.


The Rayleigh criterion is when two points are just resolved. This is when the central maximum of one image coincides with the first minimum of the other.
The minimum angular separation θ (in radians) for two points to be just resolved is given by

where λ is the wavelength and a is the diameter of the circular aperture lens receiving the image (see previous section).
FYI
Importance of resolution in technology
- CDs and DVDs: By using laser beams with shorter wavelength, we can improve resolving power of the laser and increase the amount of data stored on the discs.
- Electron microscope: Short wavelength of electrons allows electron microscopes to create images with very high resolution.
- Radio telescopes: Radio waves have long wavelengths so the aperture (satellite dish) needs to be very large for a radio telescope to achieve good resolution.
9.5 – Doppler effect
The Doppler effect for sound waves and light waves
Doppler equations for sound waves
The Doppler effect refers to the change in observed frequency of a wave due to the movement of the observer and/or that of the wave source.

There are four Doppler effect equations for observed frequency depending on different cases:
- Source moving towards observer at rest

- Source moving away from observer at rest

- Observer moving towards stationary source

- Observer moving away from stationary source

where f’ is the observed frequency of the wave emitted by the source and received by the observer, f is the original frequency of the wave, v is the velocity of the wave, and v0 is the velocity of the observer.
| Velocity of the wave | Wavelength of the wave | Frequency of the wave | |
| Moving observer | Changes | Constant | Changes |
| Moving source | Constant | Changes | Changes |
Frequency observed changes according to the equation v=fλ.
Doppler equation for electromagnetic waves

where Δf is the change in frequency of the wave received by the observer as compared to the original frequency emitted by the source, v is the velocity of the observer, c is the speed of light, and f is the original frequency of the wave.
- This equation should only be used when the velocity of the observer is much smaller than the speed of light (v<<c).< li=””></c).<>
- Add Δf to f to obtain the observed frequency (f’) when the wave source and the observer are moving towards each other.
- Subtract Δf from f to obtain the observed frequency (f’) when the wave source and the observer are moving away from each other.
Application of the Doppler effect in speed detectors:
- A beam of electromagnetic wave is fired at the car.
- The frequency of the reflected wave is compared to that of the original wave beam. A higher frequency indicates that the car is moving towards the detector and a lower frequency indicates that the car is moving away from the detector.
- The speed of the car is calculated from the extent of shift in frequency by v=fλ.
Take note that the overall difference in frequency is 2Δf from the equation because the wave travels to the car and then back to the speed detector.
Topic 10: Fields (HL)
10.1 – Describing fields
Gravitational fields
A gravitational field is a space where a small test mass experiences a force due to another mass.

Electrostatic fields
An electrostatic field is a space where a small positive test charge experiences a force per unit charge.

Electric potential and gravitational potential
Electric potential
- The electric potential is given by

or

- The electric potential difference is also known as voltage.
See section 10.2 (potential difference) for further explanation.
Gravitational potential
- The gravitational potential due to an object with mass M is given by

- The gravitational potential at a point P is equal to work done per unit mass required to take a test mass from infinity to point P.
- Gravitational potential is always negative.
- The gravitational potential at infinity is zero.
- To calculate the gravitational potential due to multiple masses, simply add up the gravitational potential due to the individual masses.
Field lines
See next section (equipotential surfaces)
Equipotential surfaces
- Points with the same gravitational potential can be joined together to form an equipotential surface

- Field lines are normal (perpendicular) to the equipotential surfaces.

- The density of field lines is proportional to the field strength.
- Far from the earth, the field line separation changes as the gravitational field strength changes. However, near the surface of the earth, the value of the gravitational field strength is relatively constant with height as long as the change of height is not too great.

10.2 – Fields at work
Potential and potential energy
Electric potential
See previous section (electric potential and gravitational potential)
Electric potential energy
- The electric potential energy is given by

were k is Coulomb’s constant, Q is the fixed charge, q is the test charge, and r is the radius.
- The electric potential energy can be defined as the capacity for doing work by a change in position of the positive test charge.
- Electric potential is also known as voltage.
Gravitational potential
See previous section (electric potential and gravitational potential)
Gravitational potential energy
- The gravitational potential energy of a system of two objects with mass M and m is given by

- The gravitational potential energy of an object at a point P is equal to the work done required to take the object from infinity to the point P.
- As gravitational forces are attractive, the work done required to bring an object from infinity to any point is negative. Thus, gravitational potential energy is always negative.
Potential gradient
- The gravitational potential gradient of a gravitational field is given by ΔV/Δr where ΔV is the change in gravitational potential between two points and Δr is the distance between those two points.
- It is the slope of a graph which plots the gravitational potential against the distance from the mass.
- Gravitational potential gradient is related to the gravitational field strength (g) by g=-ΔV/Δr=GM/r^2.
Potential difference
- The potential difference is defined as the work done by moving a positive test charge from one point to another in an electric field.
- Potential difference across an electrical component, also called voltage, is required to make a current flow through it. Cells or batteries provide the potential difference required.

Escape speed
- The escape speed of a planet is given by
![]()
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
- Escape speed it the minimum speed required for an object launched from the surface of a planet to reach infinity.
- An object launched at or above its escape speed will not return to the planet due to gravity.

Orbital motion, orbital speed and orbital energy
Orbital motion
- Gravitation provides the centripetal force for orbital motion. For example, the gravitational force between the sun and the earth provides the centripetal force for the earth to orbit the sun.
- The period of orbital motion is proportional to the average radius of the orbital motion by Kepler’s third law.

Orbital speed
- The orbital speed is given by
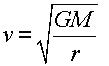
where G is the gravitational constant, M is the mass of the planet, and r is the radius of the planet.
Orbital energy
The kinetic energy, gravitational potential energy, and total energy of an orbiting satellite is given by
- Kinetic energy
![]()
- Potential energy
![]()
- Total energy = Kinetic energy + Gravitational potential energy
![]()

Forces and inverse-square law behaviour
- Inverse-square law graphical representation

- Gravitational field

- Electric field

Topic 11: Electromagnetic induction (HL)
11.1 – Electromagnetic induction
Electromotive force (emf)
- When a conducting wire moves through a magnetic field, a potential difference is created along the wire. This phenomenon is called electromagnetic induction.

- When the movement of the wire is perpendicular to the magnetic field, the emf (ε) induced is given by ε = Bvl where B is the magnetic field, v is the velocity of the wire, and l is the length of the wire.

Magnetic flux and magnetic flux linkage
- The magnetic flux through a surface measures the component of the magnetic field passing through the surface and is proportional to the number of magnetic field lines which intersect the surface.
- The magnetic flux (φ) through a surface is given by
![]()
where B is the magnetic field passing through the surface, A is the area of the surface, and θ is the angle between the magnetic field and the normal to the surface.

- The magnetic flux linkage of a coil measures the component of the magnetic field passing through the coil.
- For a coil with N turns, the total flux linkage is given by
![]()
where BA = φ = magnetic flux
Faraday’s law of induction
- Faraday’s law states that the magnitude of the induced emf is proportional to the rate of change of the flux linkage by

- Faraday’s law allows us to determine the induced emf by the change of magnetic flux over time.
Lenz’s law
- Lenz’s law states that the induced emf acts in the direction such that the current induced opposes the change which caused it.


11.2 – Power generation and transmission
Alternating current (ac) generators
- The operation of a basic alternating current (ac) generator is demonstrated in the following diagram.

- A coil of wire is driven to rotate by an external force.
- As the coil rotates, the magnetic flux linkage passing through the coil changes.
- By Faraday’s law, this induces an emf and causes current to flow within the coil.
- If the rotation is at constant speed, the induced emf is sinusoidal (recurring oscillation).
- Increasing the speed of rotation increases both the frequency and the magnitude of the induced emf.

Average power and root mean square (rms) values of current and voltage
- The average power produced (or dissipated) from an alternating current cannot be computed directly using the peak values of voltage or current.
- The root mean square (rms) value of an alternating current or voltage is the value that could be substituted into the electrical power formula P=IV to calculate the average power dissipated where I and V are rms values.

where V0 is the peak value of the alternating voltage.

where I0 is the peak value of the alternating current.

- The quoted values for alternating voltage and current refer to their rms values rather than their peak values. For an example, an ac socket in Europe is rated at 220V rms.
Transformers
- A transformer is a device which can be used to transfer electrical energy from one ac circuit to another at a different voltage.
- Transformers which increase the output voltage are called step up transformers while those which decrease the output voltage are called step down transformers.
- A transformer is essentially two coil coils of wire coupled together as shown below.

- Alternating input voltage causes constant change in the magnetic field around the primary coil.
- This causes a constant change in the magnetic flux linkage in the secondary coil.
- By Faraday’s law, an emf is induced in the secondary coil.
- The ratio between the induced input voltage (rms) and the output voltage (rms) is equal to the ratio between the number of turns in the corresponding coil.

where Vp is the voltage in the primary coil, Vs is the voltage in the secondary coil, np is the number of turns on the primary coil, and ns is the number of turns on the secondary coil.
- An ideal transformer operates at 100% efficiency. In other words, its power input is equal to power output.

since P=IV
Diode bridges
A diode bridge is an arrangement of four (or more) diodes in a bridge circuit configuration where a diode is a two-terminal electronic component that conducts current to flow in one direction.


Half-wave and full-wave rectification
Diodes are also known as rectifiers. They can be used to change alternating current (ac) to direct current (dc) through a process called rectification.
Half-wave rectification

The final dc waveform on the screen is the positive half only of the original ac waveform. In half-wave rectification, the negative part of the current is prevented from passing.
Full-wave rectification

The four diodes connected as shown in the diagram above form a full-wave rectifier. Through this arrangement, the positive half of each cycle is allowed to pass through while the negative half of each cycle is reversed. This diode configuration is commonly known as a diode bridge.
11.3 – Capacitance
Capacitance
Capacitance (C) is the ability to store change given in the unit farad (F) and can be expressed as
![]()
where C is capacitance, Q is charge, and V is voltage.

A capacitor is made up of two metallic plates with a dielectric material in between the plates.

When a voltage is applied over the two plates, an electric field is created with positive charge collecting in one plate and negative charge on the other.
This is what physicists mean when they say “a capacitor works by storing energy electrostatically in an electric field”.
The capacitance of a capacitor can be correlated to the area of the plates (A) and the distance of separation between the plates (d) by

FYI
The potential energy stored in a capacitor is given by

where E is the potential energy, Q is charge, V is voltage, and C is capacitance.
Dielectric materials
- Dielectric materials are insulators, such as glass, plastics, distilled water, dry air, or even a vacuum.
- Dielectric materials keep the conducting plates in contact, allowing for smaller plate separation (d), and higher capacitance (C).
Capacitors in series and parallel

Resistor-capacitor (RC) series circuits
An RC circuit is one where you have a capacitor and resistor in the same circuit.

The charging and discharging of an RC circuit works like this:
- Assuming that C is fully discharged and that the switch is open. When the switch is closed in position 1, the battery is connected across the capacitor. Current flows and the potential difference across the capacitor begins to rise but as more and more charge build up on the capacitor plates, the current and the rate of rise of potential difference both fall until no further current flows and the potential difference across the capacitor equals that of the supply voltage (V0). The capacitor is now fully charged.


- When the switch is then closed at position 2, a large current flows and the potential difference across the capacitor drops. As charge flows from one plate to the other through the resistor, the charge is neutralized. The current and the rate of decreasing potential difference both fall. When the charge on the plates reach zero, the initial condition, the current and potential difference are also zero. The capacitor is now fully discharged.


Time constant
The RC time constant specifies the time required to charge the capacitor, through a resistor, by approximately 63.2% or to discharge the capacitor, through a resistor, by approximately 36.8% and is given by
![]()
where τ is the RC time constant in seconds, R is the circuit resistance in ohms, and C is the circuit capacitance in farads.
Topic 12: Quantum and nuclear physics (HL)
12.1 – The interaction of matter with radiation
Photons
- Einstein proposed that light consists of particles called photons.
- Quantum refers to the smallest discrete amount of something. A photon is a quantum of electromagnetic radiation (light).
- Photons exhibit wave properties under refraction or interference.
- Photons exhibit wave properties under its emission or absorption.

- A photon’s energy (E) is proportional to its frequency (f) and is given by
![]()
where h is Planck’s constant, c is the speed of light, and λ is its wavelength (electromagnetic wave).
The photoelectric effect
- Photoelectric effect refers to the emission of electrons from a metal surface as a result of the absorption of electromagnetic wave energy.

| Factor | Effect |
| Intensity | Affects the number of electrons ejected. |
| Frequency | There exists a minimum frequency (depending on the material) below which no electrons are ejected.
Affects the maximum KE of ejected electrons |
- An example of the photoelectric effect on a sample metal surface.

Incident electromagnetic waves with lower frequency have a smaller chance of inducing the photoelectric effect.
- Why does the intensity of light affect the number of ejected electrons?
The number of photons per unit time in the incident light is proportional to the light intensity.
An increase in the intensity of the incident light allows a higher number of photon-electron interactions. Therefore, more electrons are ejected.
- Why is there a minimum frequency below which no electrons are ejected?
There exists a minimum energy below which electrons would not be ejected from the metal. This minimum energy level depends on the metal in use and is called the work function (φ).
Since E=hf, φ=hf0 where f0 is called the threshold frequency.
- How does the frequency of the incident light affect the maximum kinetic energy of the ejected electrons?
The work function corresponds to the potential energy which binds the electron to the nucleus.
Since total energy = potential energy + kinetic energy,
![]()
which may be represented on graph by the following

Matter waves
- The De Broglie hypothesis suggests that all matter exhibits wave-like properties. In particular, the momentum of a particle is related to its wavelength where the De Broglie wavelength may be deduced by the following formula

where p is momentum, h is Planck’s constant, λ is wavelength, m is mass, and v is velocity.
- The term “wave-particle duality” refers to matter acting as both waves and particles.
Pair production and pair annihilation
All matters have their antimatter counterparts which resemble their corresponding matter in every way except for the sign of their charge and the direction of their spin.
Pair production
When a high energy photon collides with a nucleus, it makes a pair of electron and positron (electron antimatter) and gives kinetic energy to each particle.

Pair annihilation
When matter collides with its corresponding antimatter, they annihilate one another with the conservation of energy, momentum, and charge.

The positron (+e) collides with the electron (-e), annihilating each other into two photons with exactly opposite directions and the same amount of momentum.
Quantization of angular momentum in the Bohr model for hydrogen
- Bohr developed a model for hydrogen that was able to explain the emission and absorption spectra of hydrogen.
- His model assumed discrete orbital paths in which electrons orbit the nucleus through, the same way planets orbit stars.
- The orbits were quantized in terms of their allowable angular momentum (rotational momentum).
- Therefore, the orbital radii and energies are also quantized.
- The energy of the orbit is the energy required to ionize (remove) an electron and can be given through the following equation in relation to the order of orbit (n)

- When the electrons are excited, they jump to higher energy orbits and eventually drop back down to a more stable orbit by releasing excess energy by the form of light. The energy of the light released is therefore equal to the difference in energy of the two orbits.
The wave function
By quantum physics, all particles do not have a defined position until they are observed. Instead, all particles are described as “a wave function”.


TL;DR: The wave function gives the probability of finding a particle at a given point which is given by the square of the amplitude of the wave function at that location.
The uncertainty principle for energy and time and position and momentum
The Heisenberg uncertainty principle states that
- If the energy state only lasts for a brief period of time, its energy is uncertain.

- Position and momentum cannot be measured simultaneously with precision. The more precisely the position is determined, the less precisely the momentum is known, and vice versa.



Tunnelling, potential barrier and factors affecting tunnelling probability
- Imagine throwing a ball at a wall and having it disappear the instant before making contact and appearing on the other side. The wall remains intact and the ball did not break through it. Believe it or not, there is a finite (if extremely small) probability that this even would occur. This phenomenon is called quantum tunnelling.

- The position of a particle is described as a wave function (see previous section).
- From the graph above, the observable particle is most likely to be at the position where its wave function has the largest amplitude. However, although the amplitude of the wave function will decay exponentially, since the wave function does not reach an amplitude of zero, the wave function can exit the barrier. Once the wave function exits the barrier, its amplitude no longer decays. This means that a particle has a certain probability of bouncing off a barrier and a certain probability of passing through the other side.
| Factor | Effect towards tunnelling probability |
| Increase barrier length | Decrease |
| Increase particle mass | Decrease |
- This explains how tunnelling is frequent in nanoscale but negligible at the macroscopic level.
12.2 – Nuclear physics
Rutherford scattering and nuclear radius
Rutherford’s undergraduate students, Geiger and Marsden, bombarded a sheet of gold foil by alpha particles.

The alpha particles passed through the gold foil in most cases, a small percentage of alpha particles were deflected by small angles of deflection, and an even smaller percentage of alpha particles were deflected by large angles of deflection.

Rutherford thus deduced that the atom consists of a small compact positive nucleus (where alpha particles deflect by large angles) with a majority of volume existing as empty space (where alpha particles pass right through).

Nuclear energy levels
- In the same way electrons can move between discrete energy levels, the nucleus of an atom can too.
- Atoms that decay through gamma decay emit distinct frequencies of gamma rays which correspond to distinct energy levels.

The neutrino
- A neutrino is a type of lepton. Since they have no electrical charge or strong charge, most neutrinos do not react with other particles and pass right through earth with no interaction.
- Neutrinos are produced in many particle decays, such as in beta decay. When a neutron at rest (zero momentum) decays by releasing a proton and an electron, because of the law of conservation of momentum, the resultant products of decay must have a total momentum of zero, which the observed proton and electron clearly does not portray. Therefore, we suggest the presence of another particle to balance the momentum – by the release of an antineutrino (neutrino antimatter). This was confirmed by experimentation.

- Neutrinos were produced in great abundance in the early universe and rarely interact with matter. This may suggest that neutrinos contribute to the total mass of the universe and affects its expansion.
The law of radioactive decay and the decay constant
Apart from half-lives (see topic 7), the activity of radioactive decay can also be shown exponentially by the law of radioactive decay.

- The decay constant (λ) represents the probability of decay of a nucleus per unit time and is dependent on the type of element.

Option B: Engineering Physics
B.1 – Rigid bodies and rotational dynamics
Torque
- When an object is acting upon by a force, it may move but it may also rotate.
- Torque is a measure of how much a force acting on an object causes that object to rotate.
- Suppose an object rotates about an axis, which we will call the pivot point ‘O’. We will call the force ‘F’. The vector distance from the pivot point to the point where the force acts is called the moment arm and is denoted by ‘r’.

- Torque may be calculated by

- When the force ‘F’ is applied perpendicular to object (θ=90), we can remove sinθ from the equation as sin90=1.
- As torque is a vector quantity, their directions must be taken into account when calculating the resultant torque.
Moment of inertia
- Just as in linear motion, mass is the tendency of a body to resist linear acceleration, the moment of inertia of an object is the tendency of a body to resist rotational acceleration.
- As torque (τ) is the rotational dynamics equivalent of force (F), moment of inertia (I) is the rotational dynamics equivalent of mass (m), the moment of inertia may be calculated by

where I is the moment of inertia, m is the mass, and r is the vector distance from the pivot point where the force acts.
- Objects of different shapes have different moments of inertia (different tendencies of it resisting rotational acceleration) due to its mass and how the mass is distributed about the axis of rotation.

Note that L is the length of the object (for cylinders and rods).
Rotational and translational equilibrium
- If an object remains at rest or continues to move in exactly the same way, it is described as being in equilibrium.
- From Topic 2, we know that translational equilibrium occurs when there is no resultant force acting on an object, so that it remains stationary or continues to move with a constant velocity.
- In rotational dynamics, rotational equilibrium occurs when there is no resultant torque acting on an object, so that it remains stationary or continues to rotate with a constant angular velocity.
- To find out whether an object is in rotational and translational equilibrium, the vector sum of forces acted upon it must be calculated such as in the following example.

Angular acceleration
From the Topic 6 in the formula booklet, we know that angular velocity may be calculated by
![]()
where ω is the angular velocity, f is the frequency of rotation, and T is the period of rotation.
As acceleration is the change in velocity over time, angular acceleration may be calculated by

where α is the angular acceleration, ω is the angular velocity, and t is time.
Equations of rotational motion for uniform angular acceleration
The equations for rotational motion are very similar to those of linear motion we previously learned in Topic 2: Mechanics.

Newton’s second law applied to angular motion
See previous section: moment of inertia


- Conservation of angular momentum
- The total angular momentum of a system is constant provided that no external torques are acting on it.
- Calculating the conservation of angular momentum is very similar to calculating the conservation of linear momentum.

FYI
Rotational kinetic energy can be calculated from

The conservation of both linear and rotational kinetic energy is useful for calculating problems like a wheel rolling down a hill (without slipping) via


B.2 – Thermodynamics
The first law of thermodynamics
The first law of thermodynamics is a statement of the principle of energy conservation

where Q is the heat (energy) added to the system, ΔU is the change in internal energy, and W is the work done by the systems.
The second law of thermodynamics
The second law of thermodynamics states that in any cyclic process, the entropy will either increase or remain the same.
This suggests that it is impossible to extract an amount of heat from a hot reservoir and use it all to do work, precluding the perfect engine.

This also suggests that it is not possible for heat to flow from a colder body to a warmer body without any work having been done to accomplish this flow. Energy will not flow spontaneously from a low temperature object to a higher temperature object, precluding the perfect refrigerator.

Entropy
Entropy in thermodynamics may be defined as a measure of the amount of energy which is unavailable to do work or a measure of the disorder of a system.
The change in entropy, ΔS, may be calculated by

Cyclic processes and pV diagrams
- A heat engine typically uses energy provided in the form of heat to do work and then exhausts the heat which cannot be used to do work. The first law is the application of conservation of energy to the system and the second sets limits on the possible efficiency of the machine and determines the direction of energy flow.
- Heat engines such as automobile engines operate in a cyclic manner, adding energy in the form of heat in one part of the cycle and using that energy to do useful work in another part of the cycle. This may be represented on a pV diagram.

- For a cyclic heat engine process, the pV diagram will be closed loop. The area inside the loop is a representation of the amount of work done during a cycle. Some idea of the relative efficiency of an engine cycle can be obtained by comparing its pV diagram with that of a Carnot cycle, the most efficient kind of heat engine cycle.
Isovolumetric, isobaric, isothermal and adiabatic processes
- An isochoric or isovolumetric process is one in which the volume of the system does not change unless there is work done on or by the system. If there is no work done on or by the system then the first law of thermodynamics becomes
ΔQ=ΔU
- In an isochoric process all the thermal energy absorbed by a system goes to increase its internal energy, this usually results in an increase in temperature. An example of an isochoric process is the heating of water in a fixed volume container. As heat is added to the water the water will begin to boil, at which point the energy supplied to the system will go into vaporizing the water.
- An isobaric process is one in which the pressure of the system is constant. The heat energy added to the system does work and increases the internal energy of the system. An example could be forcing the air out of a piston slowly so that the pressure is constant throughout the piston.
- An isothermal process is one in which the temperature of the system is constant. It is possible to compress gas with a piston slowly so that the temperature of the gas itself does not change. The process is done slowly to allow the heat to transfer to the surroundings. If there is no phase change the lack of temperature change implies that there is no change in the internal energy of the gas or system. Thus we can write the first law of thermodynamics as
ΔQ=ΔW
- So all energy added to the system results in work being done by the system, or if work is done on the system heat energy leaves the system. During an isothermal process the value of pV is constant.
- An adiabatic process is one in which there is no exchange of thermal energy between a system and it surroundings (Q=0). Thus, for an adiabatic process the first law of thermodynamics becomes
ΔW=−ΔU
- In other words all the work done is at the expense of the system’s internal energy. An example of an adiabatic process is gas in an insulated piston, where the gas quickly expands and does work on the piston. This results in a decrease in internal energy and is most often accompanied by a drop in temperature.
- As no heat enters or leaves the system in an adiabatic process, it can be shown that, if the state of a fixed quantity of an ideal gas is changed from pressure p1 and volume V1 to p2 and V2,



The different colored lines in the bottom two diagrams represent different temperatures where a movement on a single color curve represents constant temperature and a shift across different color curves represent a shift of temperature.
FYI
Calculating the internal energy of the system
For monatomic gases, gases which occur as single atoms such as helium and argon (in contrast to diatomic gases such as hydrogen, oxygen, and nitrogen), under ideal gas conditions, their internal energy may be given by

where U is the internal energy of the monatomic ideal gas, n is the number of moles, R is the universal gas constant, and T is the temperature in Kelvin.
Calculating work done by the system
To calculate the work done by a gas at a non-constant pressure we must employ integration (calculus). In simple terms, integration finds the area between a curve and the x-axis. What we find is that the work done by a gas can be found from a pV diagram by finding the area under the curve.

From this we can see the work done by an isobaric process is
W=pΔV
For an isochoric process the work done is
W=0
There volume does not change, no work is done, and all energy transfer is involved in internal energy or heat exchange.
For isothermal and adiabatic processes the work done is more complicated, but is still represented by the area under the curve.
Carnot cycle
During one part of the cycle performed in an engine, some heat is absorbed from a hot reservoir. During another part, a smaller amount of heat is rejected to a cooler reservoir. The engine is therefore said to operate between these two reservoirs. It is a fact of experience that some heat is always rejected to the cooler reservoir.
The most efficient heat engine cycle is the Carnot cycle, consisting of two isothermal processes and two adiabatic processes. The Carnot cycle can be thought of as the most efficient heat engine cycle allowed by physical laws.
The Carnot cycle has four steps:

A to B – The gas expands isothermally, while heat energy is added to the gas.
B to C – The gas expands adiabatically. Volume reaches a maximum and the pressure reaches a minimum.
C to D – The gas is compressed isothermally, while heat energy is dumped into a cold reservoir.
D to A – The gas is compressed adiabatically, Volume reaches a minimum and the pressure is maximum.


Thermal efficiency
The thermodynamic efficiency, η, of the engine may be defined as
![]()
where W is work done and Q is energy as W=Qin-Qout.
As the efficiency increases, the difference between the temperatures in the hot and cold reservoirs increases. At the theoretical maximum efficiency (Carnot cycle),

where Tcold is the temperature in the cold reservoir and Thot is the temperature in the hot reservoir.
Option B: Engineering Physics (HL)
B.3 – Fluids and fluid dynamics
Density and pressure
Density may be defined as
![]()
where ρ is density, m is mass, and V is volume.
Pressure may be defined as
![]()
where P is pressure, F is the force applied, and A is the area of the object in which the force is applied upon.

This equation can be applied to any static fluid in any shaped container, or no container. The equation shows that, for a given fluid, the pressure depends only on depth (assuming we are referring only to locations where g is constant).
Thus,


Buoyancy and Archimedes’ principle

Thus, when an object is wholly or partially immersed in a fluid, it experiences an upthrust (buoyancy force) equal to the weight of the fluid displaced. This is Archimedes’ principle.

Pascal’s principle
Because any liquid is incompressible (its volume cannot be reduced) and its molecular motions are random, we can state that a pressure exerted anywhere in an enclosed static liquid will be transferred equally to all other parts of the liquid.
If different parts of the liquid are at different heights, however, this will result in additional differences in pressure, which may or may not be significant. This is the basis of hydraulic machinery.

Hydrostatic equilibrium
A fluid is in hydrostatic equilibrium if it is either at rest or if any parts of it that are moving have a constant velocity.
This will occur when forces are balanced by differences in pressure. For example:
- A floating boat will be in a state of hydrostatic equilibrium if it is balanced by pressure differences in the water.
- The Earth’s atmosphere (as a whole) is in hydrostatic equilibrium because pressure differences cross the atmosphere are balancing the effects of gravity on the air.
- Most stars are in hydrostatic equilibrium because the inwards gravitational attraction between the particles is opposed by the outwards pressure of the hot gases and radiation.
The ideal fluid
We can idealize and simplify the flow of a fluid as the movement of layers sliding over each other (like playing cards sliding over each other), without any movement of fluid between those layers. This is described as laminar flow.

Thus, an ideal fluid
- has constant density and is incompressible
- has constant pressure, acting equally in all directions
- is non-viscous meaning that it has no frictional forces opposing motion. There are no shear forces between layers, or frictional forces between layers or any surfaces with which they may come in contact. (Shear forces are non-aligned parallel forces that tend to push a substance in opposite directions.)
- has a steady flow pattern that does not change with time and which can be represented by streamlines.
Streamlines
- Streamlines are lines that show the paths that (mass-less) objects would follow if they were placed in the flow of a fluid. The arrows in the picture above (in the previous section) represent streamlines.
- A tangent to a streamline shows the velocity of flow at that point.
- Streamlines cannot cross over each other.
- If the streamlines get closer together, the fluid must be flowing faster.
- Smoke or dye are often used in labs to mark the streamlines.
The continuity equation
The mass per second entering and leaving the tube must be constant and, because the fluid is incompressible, the flow speed must increase where the tube’s cross-sectional area decreases.


The Bernoulli equation and the Bernoulli effect
The Bernoulli equation
In general, we would expect that the speed of flow of an incompressible fluid in an enclosed system would increase if
- some kind of pump was providing a pressure difference
- the pipe was going down to a lower level
- the pipe was getting narrower.
The Bernoulli equation involves these factors in an equation that describes the steady flow of an ideal fluid in any system and may be given by

(h is represented by z in the formula booklet)



The Bernoulli effect
For a fluid flowing horizontally (or with insignificant height variations), the Bernoulli equation reduces to 1/2ρv^2 + p = constant.
This shows us that if an (ideal) fluid is flowing horizontally, or an object is moving horizontally through a fluid without turbulence, there must be a decrease in pressure wherever the speed increases.
This is commonly known as the Bernoulli effect and it has many interesting applications such as
- The curved path of spinning balls – The motion of the ball’s surface will increase the speed of the air flow on one side and decrease it on the other. This effect will be greater if the surface of the ball is not smooth. The difference in air speeds causes a pressure difference and a force in one direction.

- Aircraft wings – The cross-sectional shape of an aircraft wing (called its aerofoil or airfoil) will affect the way in which the air flows past it. If the shape causes the streamlines to be closer together above the wing, this increases the speed of the air and reduces the pressure, causing an upwards force called lift. The effect may be increased by raising the leading edge of the aerofoil; this also causes the force of the air striking the aerofoil to have a vertical component, increasing lift.

- Venturi tubes – A fluid flowing through a tube will have less pressure at a place where the tube is narrower because the fluid must flow faster. Thus, measuring the decrease in pressure caused by a Venturi tube can be used to determine a fluid’s flow rate.

The Venturi effect can be very useful in situations where fluids need to be mixed. A narrowing in a tube with one fluid flowing though it can produce a decrease in pressure that encourages another fluid to flow into the tube. For example, this is used in car engines to mix air and gasoline (petrol).
Stokes’ law and viscosity
Viscosity
Contrary to our assumptions of an ideal fluid, no liquid is perfectly ideal because there will always be some frictional forces between different layers and the outer layers and any container. Thus, viscosity can be considered as a measure of a fluid’s resistance to flow.
Stokes’ law
When an object moves through a fluid it will experience a resistive force because of the viscosity of the fluid. This force is known as viscous drag. Stokes’s law provides a way of calculating the size of this drag force given that
- there must be streamline (laminar) flow
- spherical objects are used as test objects (drag force experienced by spheres)
- the test objects have smooth surfaces.

where F is the drag force experienced by the test object (sphere), η is the coefficient of viscosity (different for different fluids), r is the radius of the sphere, and v is the velocity in which the test objects travels.
Laminar and turbulent flow and the Reynolds number
- For laminar and turbulent flow, see previous section (The ideal fluid).
- As the mean speed, v, of a fluid through a pipe of radius r increases, laminar flow becomes less likely and turbulence may begin. The Reynolds number, R, is used as a guide to predict the conditions under which turbulent (non-laminar) flow will begin which may be given by

where v is the mean speed of a fluid through a pipe, r is the radius of the pipe, ρ is the density of the fluid, and η is the coefficient of viscosity of the fluid.
- This equation demonstrates that a fluid can flow faster without causing turbulence if it has a larger viscosity and smaller density, and if larger dimensions are involved. The same equation can be used for estimating the maximum speed of an object of dimension r through a stationary fluid before turbulence will begin.
- Turbulence is often characterized by swirling currents, involving some flow in the opposite direction to most of the fluid. These are known as vortices and eddies. The alternate formation of vortices can result in oscillation forces on an object situated in a fluid flow, which can give rise to resonance effects.
- According to the syllabus, values where R<10^3 represent conditions for laminar flow.
B.4 – Forced vibrations and resonance
Natural frequency of vibration
- When something is disturbed and then left to oscillate without further interference, it is said to oscillate at its natural frequency of (free) vibration.
- An object made of only one material in a simple shape, a tuning fork for example, may produce a single natural frequency, but objects with more complicated structures will have a range of natural frequencies although one frequency may dominate.
Q-factor and damping
Damping
The motions of all objects have frictional forces of one kind or another acting against them. Frictional forces always act in the opposite direction to the instantaneous motion of an oscillator and result in a reduction of speed and the transfer of kinetic energy (and, consequently, potential energy). Therefore, as with all other mechanical systems, useful energy is transferred from the oscillator into the surroundings (dissipated) in the form of thermal energy and sound. Consequently, an oscillator will move at slower and slower speeds, and its successive amplitudes will decrease in size. This effect is called damping.

There are various types of damping such as where
- some oscillations are over-damped because of considerable frictional forces. In effect no oscillations occur because resistive forces are such that the object takes a long time (compared to its natural period) to return to its equilibrium position. The decrease in amplitude with time is often exponential.
- conversely, occasionally damping can be very light and the oscillator may continue to oscillate, taking some time to dissipate its energy. A pendulum and a mass oscillating on a spring are good examples of under-damped systems. If the mass on the spring was placed in a beaker of oil (instead of air) it may then become over-damped.
- oscillations are often unhelpful or destructive and we may want to stop them as soon as possible. If an oscillation is stopped by resistive forces, such that it settles relatively quickly (compared to its natural period) back into its equilibrium position, without ever passing through it, the process is described as critically damped. A car’s suspension is an example of this kind of damping, as are self-closing doors.
Q-factor
We have seen that the amplitude, A, of a damped oscillator decreases approximately
exponentially with time. The Q (quality) – factor of an oscillator is a way of representing the degree of damping involved. A high Q-factor means that there is little damping.

where (one) cycle means (one) oscillation.
The Q factor for critical damping is usually quoted to be about 0.5, which suggests that most of the energy of the oscillator is dissipated in much less than one time period.
Periodic stimulus and the driving frequency
- A forced oscillation occurs when an external oscillating force acts on another system tending to make it oscillate at a frequency that may be different from its natural frequency.
- The most important examples of forced oscillation are those in which the frequency of the external force (often called the driving frequency or the forcing frequency) is the same as the natural frequency. The child on the swing is an example of this. When a regular periodic stimulus to a system results in an increasing amplitude, the effect is called resonance.
Resonance
Resonance is the increase in amplitude and energy of an oscillation that occurs when an external oscillating force has the same frequency as the natural frequency of the system. The oscillations of the driving force must be in phase with the natural oscillations of the system.
There are many important examples of resonance. Some are useful but many are unwanted and we usually try to reduce their damaging effects. Avoiding resonance in all kinds of structures is a major concern for engineers and it is an interesting combination of physics theory and practical engineering.
Some types of useful resonance may be where
- The molecules of certain gases in the atmosphere oscillate at the same frequency as infrared radiation emitted from the Earth. These gases absorb energy because of resonance; this results in the planet being warmer than it would be without the gases in the atmosphere. This is known as the greenhouse effect
- Radios and TVs around the world are ‘tuned’ by changing the frequency of an electronic circuit until it matches the driving frequency provided by the transmitted signal.
- Your legs can be thought of as pendulums with their own natural frequency. If you walk with your legs moving at that frequency, energy will be transferred more efficiently and it will be less tiring (we tend to do this without thinking about it).
- Quartz crystals can be made to resonate using electronics – the resulting oscillations are useful in driving accurate timing devices such as watches and computers.
- The sound from musical instruments can be amplified if the vibrations are passed on to a supporting structure that can resonate at the same frequency. An obvious example would be the strings on a guitar causing resonance in the box on which they are mounted. Because the box has a much larger surface area it produces a much louder sound than the string alone.
- Magnetic resonance imaging (MRI) is a widely used technique for obtaining images of features inside the human body. Electromagnetic waves of the right frequency (radio waves) are used to change the spin of protons (hydrogen nuclei) in water molecules.
Some types of unwanted resonance may be where
- Parts of almost all engines and machinery (and their surroundings) might vibrate destructively when their motors are operating at certain frequencies. For example, a washing machine may vibrate violently when the spinner is running at a certain frequency, and parts of vehicles can vibrate when the engine reaches a certain frequency, or they travel at certain speeds.
- Earthquakes may well affect some buildings more than others. The buildings that are most damaged are often those that have natural frequencies close to the frequencies of the earthquake.
- Strong winds or currents can cause dangerous resonance in structures such as bridges and towers. This is often due to the effect of eddies and vortices as the wind or water flows around the structure
To reduce the risk of damage from resonance, engineers can
- alter the shape of the structure to change the flow of the air or water past it.
- change the design so that the natural frequencies are not the same as any possible driving frequencies – this will involve changing the stiffness and mass of the relevant parts of the structure.
- ensure that there is enough damping in the structure and that it is not too rigid, so that energy can be dissipated.
Option D: Astrophysics
D.1 – Stellar quantities
Objects in the universe
The solar system is comprised of the Sun, eight planets, several dwarf planets, numerous moons, and hundreds of thousands of other material left over from the construction of the solar system such as asteroids and comets.


However, the solar system in which we live in is merely a speck of dust in the vast universe.
Single star: A luminous sphere of plasma held together by its own gravity.
Binary star: Two stars orbiting a common center.
Black hole: A singularity in space-time.
Cepheid variable: A star with a period of varying luminosity. The luminosity can be determined from the period and along with the apparent brightness can be used to determine the distance of the star from Earth.
Clusters of galaxies: Two or more galaxies that are close enough to each other to affect each other through gravitation.
Constellation: A pattern of stars visible from Earth that are not gravitational bounded.
Dark matter: Matter in galaxies that are too cold to radiate. Its existence is inferred from theoretical physics rather than direct visual contact.
Galaxies: stars, gas, and dust held together by gravitational forces.
Main sequence star: A normal star that is undergoing nuclear fusion of hydrogen into helium.
Neutron stars: A very dense star, consisting only of uncharged neutrons. Nebula: A cloud of dust, hydrogen, helium and other ionized gases.
Planet: A celestial body that orbits a star.
Planetary system: Gravitationally bounded non-stellar objects in orbit around a star or star system.
Planetary nebula: The ejected envelope of a red giant star.
Stellar clusters: A group of stars gravitationally bounded together.
The nature of stars
The stability of a star depends on the equilibrium between two opposing forces. The equilibrium depends on the gravitation which can collapse the star and the radiation pressure which can make the star expand. This equilibrium is gained through nuclear fusion which provides the energy the star needs to keep it hot so that the star’s radiation pressure is high enough to oppose gravitational contraction.

Apart from single stars like the Sun, there are many types of stars in our universe (see previous section).
Astronomical distances
Our universe is composed of mostly empty space with occasional encounters of matter apart large distances.
A light year is a unit of measurement of ultra-solar system distances. It’s the distance traveled by light in one year. The speed of light is 3*10^8m/s. You can find out the number of seconds in a year by multiplying the number of seconds in a minute (60) by the number of minutes in an hour (60), then multiplying that by the number of hours in a day (24) and multiplying that by the number of days in a year (approximately 365.25). One light year is thus approximately equivalent to 9.46 x 10^15m, which is also approximately equivalent to 0.3068 parsecs (pc).
Example: The distance to the nearest star other than the Sun (Proxima Centauri) from the Earth is 4.31 light years, which is equivalent to 1.3pc. This means that it would take 4.31 years to send or receive a message to/from Proxima Centauri by electromagnetic wave transmission.
The average distance between stars in a galaxy is approximately 1 pc, which is equivalent to 3.26 light years. The average distance between galaxies within the same cluster ranges from 100 kpc (kiloparsecs) to several hundred kpc. Galaxies in different clusters can be up to a few mpc (megaparsecs) apart. 1 mpc is equivalent to 1000 kpc.
To recognize the scale of the universe compared to common objects, see the link below.
Stellar parallax and its limitations
Stellar parallax is a term used to describe the distance between two objects in space. When an observer on Earth photographs a relatively nearby star against a background of distant stars on two different occasions six months apart, the target star image will appear to have shifted against the more distant stellar background.


The baseline shift of the observer on Earth is 2 astronomical units (AU). By convention, calculations are normalized to one AU, the radius of the Earth’s orbit, so one half of the measured shift in apparent position is deemed the “parallax” of the target.
A parallax of one arcsecond is called a parsec. Since we know, the radius of the Earth’s orbit, simple Euclidean geometry allows us to calculate that a star exhibiting a one arcsecond shift is 3.26 light years or one parsec away from Earth.
However, if a star is too far away from Earth, its parallax will be too small to be measured with accuracy.
Luminosity and apparent brightness
The total power radiated by a star in all directions is known as its luminosity and the SI unit for luminosity is watts ( W ). When you compare this to the power received by an observer on the Earth, you can see that the two quantities are quite different. The power received per unit is known as the star’s brightness and this is measured in watts per metre squared (W/m^2).
If two stars were at the same distance from Earth, the one that had the greatest luminosity would also have the greatest brightness. However, because stars are at different distances from the Earth, their brightness will depend on the luminosity as well as the distance from Earth. The luminosity of a star will decrease with distance according to the inverse square law.

D.2 – Stellar characteristics and stellar evolution
Stellar spectra
The stellar spectra can be used to identify elements in stars.
Most stellar spectra use the absorption spectrum which is a continuous spectrum that passes through a cool gas and has specific spectral lines removed (inverse of an emission spectrum). The missing wavelengths in a star’s absorption spectra correspond to the absorption spectrum of a number of elements in the star.
There are 7 basic spectral classes: O, B, A, F, G, K and M.
| Class | Surface temperature (K) | Color |
| O | 28000-50000 | Blue |
| B | 9900-28000 | Blue-white |
| A | 7400-9900 | White |
| F | 6000-7400 | Yellow-white |
| G | 4900-6000 | Yellow |
| K | 3500-4900 | Orange |
| M | 2000-3500 | Orange-red |
As temperature increases, electrons are kicked up to higher levels by collisions with other atoms. Large atoms have more kinetic energy, and their electrons are excited first, followed by lower mass atoms.

If the collision is strong enough (high temperatures) then the electron is knocked off the atom and we say that the atom is ionized. So as we go from low temperatures in stars (a few thousand Kelvins), we see heavy atoms, like calcium and magnesium, in the stellar spectra. For stars with higher temperatures, we see lines from lighter atoms, such as hydrogen. The heavier atoms are all ionized by this point and have no electrons to produce absorption lines.

Hertzsprung–Russell (HR) diagram
The Hertzsprung-Russell (HR) diagram shows the relationship between absolute magnitude, luminosity, classification, and surface temperature of stars.

Most of the stars occupy the region along the line called the main sequence. During this stage, stars are burning hydrogen.
The H-R diagram is also used by scientists to help the figure out roughly how far away the stars are from Earth. This can be done because if we know the apparent magnitude, we can plot the star onto the graph using its spectral class and the type of star it is. We can then use the graph to deduce the absolute magnitude of the star.
Mass–luminosity relation for main sequence stars
For main sequence stars, the luminosity increases with the mass with the approximate power law

where L⊙ and M⊙ are the luminosity and mass of the Sun. The value a = 3.5 is commonly used for main-sequence stars and does not apply to red giants or white dwarfs.
Cepheid variables
Cepheid variables are stars in which its luminosity increases sharply and falls gently in a period of time. Thus, the period is correlated to the luminosity of the star and the Cepheid variable can be used to estimate the distance of the star.
Cepheid variables on a luminosity-period graph, due to their brightness increase and gradual fade offs, curves on the graph, giving a sine graph picture. The outer layers of the star go through contractions and expansions periodically. When it expands outward, the star becomes brighter because of high velocity, and when it contracts, the star becomes dimmer as the surface it moves inward.


Cepheid variables are thousands of times more luminous than the Sun and provide us with such a benchmark which is known in astronomy as a “standard candle”.
Stellar evolution on HR diagrams
The nebulae in space from which stars are created are actually the remains of a previous star that has reached the end of its lifecycle and died. Generally speaking, they consist of hydrogen and helium and small amount of the other heavier elements. The nebula, under the influence of gravity, begins to condense, and eventually, a protostar is formed. Such protostars can be observed in nebulas such as the horsehead nebula and the crab nebula. It is in this stage that the process of nucleosynthesis begins. Nucleosynthesis, in contrast to the nuclear processes that we are used to on Earth, is fusion, not fission. That is, instead of splitting a heavy nucleus, light nuclei are smashed together and fuse to produce a heavier nucleus, and gamma rays. It is called the proton-proton cycle. The star will continue to react its core of hydrogen into helium for all of its main-sequence lifetime (see previous section: the nature of stars).
Once the star runs out of hydrogen, the core collapses, and, under the additional gravitational pressure, the hydrogen in the core will start to undergo fusion. This causes the outer layers of the star to expand, however, the outer layers also cool, and the star becomes a red giant. The core continues to react and elements such as carbon, neon, oxygen, silicon and iron are produced. It is here that the elements that compose our world are created. Without the stars then universe would be composed of hydrogen and little else.
When the star finally runs out of fuel completely; usually when the core becomes iron, the red giant star collapses. The next stage of the star is determined by the mass of that star and the Chandrasekhar limit.
If a star is below 1.4 solar masses (Type G), it is less that the Chandrasekhar limit and when it collapses, its forms a white dwarf of 1.4 solar masses or less, along with a planetary nebula. The white dwarf star continues to cool and eventually becomes invisible.
If a star is above 1.4 solar masses (Type A, B, O), it is above the Chandrasekhar limit and instead of becoming a regular red giant, it becomes a super red giant. In this case, when the star dies, it takes a rather more spectacular path than the star below the Chandrasekhar limit, becoming a supernova. Depending on the mass of the star, it will either go on to become a black hole or a neutron star.
For stellar masses less than about 1.4 solar masses, the energy from the gravitational collapse is not sufficient to produce the neutrons of a neutron star so the collapse is halted by electron degeneracy to form white dwarfs. Electron degeneracy is a stellar application of the Pauli Exclusion Principle, as is neutron degeneracy. No two electrons can occupy identical states, even under the pressure of a collapsing star of several solar masses.

H-R diagrams can also be used to plot the evolution of a star from its birth as a protostar until its death as a white dwarf.

Red giants, white dwarfs, neutron stars and black holes
See previous section.
Chandrasekhar and Oppenheimer–Volkoff limits
Chandrasekhar limit
The largest mass a white dwarf can have is about 1.4 solar masses.
Oppenheimer-Volkoff limit
Oppenheimer-Volkoff limits the largest mass a neutron star can have to approximately 2-3 solar masses. The uncertainty in this limit comes from the fact that the equation of state of the matter inside a neutron star is not precisely known.
D.3 – Cosmology
The Big Bang model
The Big Bang theory states that both space and time originated with the expansion from a singularity.

The evidence that supported the Big Bang theory was observed through the redshift (Doppler effect) of almost all the galaxies. This indicates that all of the galaxies are moving away from us.
Although that observation would seem to indicate that we, or rather, the Earth, are at the centre of the universe, this is not the case. It only appears to be this way as we are observing from the Earth. If we were on a different galaxy, we would see our own galaxy moving away in the same manner as we are observing that galaxy moving away. This can be related to the idea of painted dots on the surface of a balloon; as the balloon is inflated, all of the dots move away from each other equally.
Ultimately, however, what gave the Big Bang theory weight above all others was the discovery of the Cosmic Microwave Background radiation.

This discovery supports the Big Bang theory in two major ways:
- The early universe was in thermal equilibrium and the radiation from then had a black body spectrum, which has traveled through space, becoming increasingly redshifted up to this point in time. This reduces the temperature of the black body spectrum and the radiation should be visible from every point in space.

- As the radiation travels throughout the universe, space has expanded, causing the wavelength to increase and its energy to decrease.
All these observations are in accordance with the Big Bang theory.

Cosmic microwave background (CMB) radiation
See previous section.
Hubble’s law
Hubble’s law states v = Hd, where v is the speed, H is the Hubble parameter, and d is the distance. It describes Hubble’s observation, that most lines in the spectra of other galaxies were redshifted where the amount of shift was approximately proportional to the distance of the galaxy from us. Thus, the velocity is proportional to the distance.
We can use Hubble’s law to estimate the age of the universe.

However, Hubble’s law really describes the speed at which celestial bodies move away from each other at the present time and changes because the expansion of the universe if accelerating.
The accelerating universe and redshift (z)
The evidence for an accelerating expansion comes from observations of the brightness of distant supernovae. We observe the redshift of a supernova which tells us by what the factor the Universe has expanded since the supernova exploded. This factor is (1+z), where z is the redshift. However, in order to determine the expected brightness of the supernova, we need to know its distance now. If the expansion of the Universe is accelerating due to a cosmological constant, then the expansion was slower in the past, and thus the time required to expand by a given factor is longer, and the distance now is larger. But if the expansion is decelerating, it was faster in the past and the distance now is smaller. Thus for an accelerating expansion, the supernovae at high redshifts will appear to be fainter than they would for a decelerating expansion because their current distances are larger.
The cosmic scale factor (R)
The cosmic scale factor is a function of time which represents the relative expansion of the universe.
This may be represented by
![]()
where d(t) is the proper distance at time t, d0 is the distance at time t0, and a(t) is the cosmic scale factor.
Astrophysicists would out the cosmic scale factor using Einstein’s theory of general relativity laws.
FYI
Option D: Astrophysics (HL)
D.4 – Stellar processes
The Jeans criterion
Stars form when a portion of interstellar cloud collapses gravitationally.
The Jeans mass criterion is determined by asking when the magnitude of the gravitational potential energy exceeds the magnitude of the gas’s kinetic energy.
The collapse of an interstellar cloud may begin if M>Mj where Mj is the Jeans criterion.

Nuclear fusion
Nucleosynthesis is the process of combining light elements into heavier elements, also known as fusion. Nucleosynthesis requires high speed collisions and high temperatures. Temperatures in the core are much higher than on the surface of a star. The main process for energy production in a star is nuclear fusion of hydrogen to helium. This is the process that occurs during most of a star’s lifetime. After the hydrogen in the star’s core is exhausted, the star can burn helium to form progressively heavier elements, carbon and oxygen and so on, until iron and nickel are formed. Up to this point the process releases energy. The formation of elements heavier than iron and nickel requires the input of energy. Supernova explosions result when the cores of massive stars have exhausted their fuel supplies and burned everything into iron and nickel. The nuclei with mass heavier than nickel are thought to be formed during these explosions.
All stars follow a simple proton-proton cycle in order to maintain equilibrium between gravity and pressure. When the star is expanding, it rises in temperature and therefore rises in pressure. This is required in order to keep a balance between the force of gravity that is trying to compress the star. At the beginning of a star’s life cycle the star consists mainly of hydrogen; in fact they are 98% made of hydrogen. There are three basic stages of the proton-proton cycle:
- Two hydrogens fuse to form deuterium plus a positron and a neutrino. Each positron is annihilated to create 2 gamma particles which are in turn absorbed and re-emitted as 200,000 photons of light per gamma particle.
- A deuterium and a hydrogen fuse to create helium and a gamma particle. Another deuterium and a hydrogen fuse to create helium and a gamma particle. Thus far, there have been 4 gamma particles created with 800,000 photons of light. That’s one bright star!
- Two helium atoms fuse to create a heavy helium atom. Once the hydrogen in the star runs out, it begins to consume the created helium from hydrogen reactions. Based on the star’s color, you can find out what type of fuel it’s consuming. This is where the Hertzsprung-Russell diagrams were derived from (see later section).

Nucleosynthesis off the main sequence
Clouds of hydrogen and helium form into main sequence stars, where nuclear fusion takes place, fusing hydrogen to form helium. Further fusion only takes place in heavier stars, otherwise the pull of gravity forces the star to contract and cool to a red dwarf. If further fusion takes place, the star becomes a red giant.
Red giants are formed when the hydrogen in the core of the star has fused into heavier helium and helium fusions occur to create beryllium. Gravity causes the star to contract and heat up. The hydrogen around the core burns more fiercely and causes the outer part of the star to expand and cool down. Small red giants (1.4 solar masses – Chandrasekhar limit) cannot withstand the pull of gravity, so it shrinks, becomes extremely hot, until it finally cools into a white dwarf. Larger red giants fuses until iron is formed, however, further fusion cannot take place without energy input. Therefore, the star contracts and heat up because of the large kinetic energy in the particles and explode as a supernova, spilling its rich elements into space to form future stars and planets

Type Ia and II supernovae
Type Ia supernova
Type Ia supernovae occur in a binary system — two stars orbiting one another. One of the stars in the system must be a white dwarf star, the dense, carbon remains of a star that was about the size of our Sun. The other can be a giant star or even a smaller white dwarf.
White dwarf stars are one of the densest forms of matter, second only to neutron stars and black holes. Just a teaspoon of matter from a white dwarf would weigh five tons. Because white dwarf stars are so dense, their gravity is particularly intense. The white dwarf will begin to pull material off its companion star, adding that matter to itself.
When the white dwarf reaches 1.4 solar masses, or about 40 percent more massive than our Sun, a nuclear chain reaction occurs, causing the white dwarf to explode. The resulting light is 5 billion times brighter than the Sun.
Because the chain reaction always happens in the same way, and at the same mass, the brightness of these Type Ia supernovae are also always the same. To find the distance to the galaxy that contains the supernova, scientists just have to compare how bright they know the explosion should be with how bright the explosion appears. Using the inverse square law, they can compute the distance to the supernova and thus to the supernova’s home galaxy. Thus, Type Ia supernovae are also known as “standard candles”.
Type II supernova
Most stars that are eight or more times the mass of our sun die as a Type II Supernova. A Type II Supernova is a supernova that is classified as having hydrogen lines in its spectra that are made by the explosion of a very large star. The hydrogen lines come from the hydrogen-rich outer layers of the star as the star explodes.

The top shows the evolution of a Type Ia supernova while the bottom shows the evolution of a Type II supernova.
D.5 – Further cosmology
The cosmological principle
The idea of a uniform universe is called the cosmological principle. There are two aspects of the cosmological principle:
- The universe is homogeneous. This means there is no preferred observing position in the universe (everywhere looks the same). However, homogenous does not mean that all regions of space should appear identical or be smoothly filled with particles. It only means that the same types of structures — stars, galaxies, clusters, and superclusters — are seen everywhere.
- The universe is also isotropic. This means you see no difference in the structure of the universe as you look in different directions. In other words, no observation can be made that will identify an edge or a center. The concept of isotropy is supported by the fact that galaxies do not bunch up in any direction in the sky and by the fact that we observe the same Hubble relation in different directions in the sky. Large telescopes have been used to count faint and distant galaxies in different direction and the numbers are always statistically the same.


Rotation curves and the mass of galaxies
How do we measure the amount of mass in the universe? We measure gravity, indirectly by measuring motion and applying Newton’s law of gravity.
The orbital period of the Sun around the galaxy gives us a mean mass for the amount of material inside the Sun’s orbit. A detailed plot of the orbital speed of the galaxy as a function of radius reveals the distribution of mass within the galaxy. The simplest type of rotation is wheel rotation shown below.

Rotation following Kepler’s 3rd law is shown above as planet-like or differential rotation. Notice that the orbital speeds falls off as you go to greater radii within the galaxy. This is called a Keplerian rotation curve.
However, plotting the curves of observed data points, the rotation curve of the galaxy stays flat out to large distances, instead of falling off as predicted in the figure above (planet-like rotation). This means that the mass of the galaxy increases with increasing distance from the center (radius).

The surprising thing as there is very little visible matter far beyond the center of the galaxy. The rotation curve of the galaxy indicates a great deal of mass but these masses cannot be observed. In other words, the halo of our galaxy is filled with a mysterious matter of unknown composition and type known as dark matter.

Dark matter
Roughly 80 percent of the mass of the universe is made up of material that scientists cannot directly observe. Known as dark matter, this bizarre ingredient does not emit light or energy. Most scientists think that dark matter is composed of non-baryonic matter. The lead candidate, WIMPS (weakly interacting massive particles), have ten to a hundred times the mass of a proton, but their weak interactions with “normal” matter make them difficult to detect.
Fluctuations in the CMB
Although the temperature of the CMB is almost completely uniform at 2.7K, there are very tiny variations, or anisotropies, in the temperature on the order of 10^-5K. The anisotropies appear on the map as cooler blue and warmer red patches. But what do these minute fluctuations mean?
These anisotropies in the temperature map correspond to areas of varying density fluctuations in the early universe. Eventually, gravity would draw the high-density fluctuations into even denser and more pronounced ones. After billions of years, these little ripples in the early universe evolved, through gravitational attraction, into the planets, stars, galaxies, and clusters of galaxies that we see today.

The cosmological origin of redshift
During the first 380000 years after the Big Bang, the universe was so hot that all matter existed as plasma. During this time, photons could not travel undisturbed through the plasma because they interacted constantly with the charged electrons and baryons, in a phenomenon known as Thompson Scattering. As a result, the universe was opaque.
As the universe expanded and cooled, electrons began to bind to nuclei, forming atoms. The introduction of neutral matter allowed light to pass freely without scattering. This separation of light and matter is known as decoupling. The light first radiated from this process is what we now see as the Cosmic Microwave Background.
The CMB is a perfect example of redshift. Originally, CMB photons had much shorter wavelengths with high associated energy, corresponding to a temperature of about 3000K. As the universe expanded, the light was stretched into longer and less energetic wavelengths. By the time the light reaches us, 14 billion years later, we observe it as low-energy microwaves at a frigid 2.7K. This is why CMB is so cold now.


Critical density
The more mass there is, the more gravity there is to slow down the expansion. Is there enough gravity to halt the expansion and recollapse the universe or not? If there is enough matter (gravity) to recollapse the universe, the universe is “closed’”. A closed universe would be shaped like a four-dimensional sphere (finite, but unbounded). Space curves back on itself and time has a beginning and an end. If there is not enough matter, the universe will keep expanding forever. Such a universe is “open”‘. An open universe would be shaped like a four-dimensional saddle (infinite and unbounded). Space curves away from itself and time has no end.

Instead of trying to add up all of the mass in the universe, a more reasonable thing to do is to find the density of a representative region of the universe where density=(mass in the region)/(volume of the region). If the region is truly representative, then the total mass of the universe=(the density)*(the total volume of the universe). If the density is great enough, then the universe is closed. If the density is low enough, then the universe is open. In the popular astronomy magazines, you will probably see the mass density of the universe specified by the symbol “W”, also known as the ratio of the current density to the “critical density” described in the next paragraph. If W < 1, the universe is open; if W > 1, the universe is closed.

Critical Density
The boundary density between the case where the universe has enough mass/volume to close universe and too little mass/volume to stop the expansion is called the critical density, which may be represented as

where H is the Hubble constant for a given cosmological time (such as the present). The current critical density is approximately 1.06*10^-29g/cm^3. This amounts to six hydrogen atoms per cubic meter on average overall.
A critical density universe has “flat” curvature. The W density parameter equals to exactly 1 in a flat universe. It is to be noted that the Hubble “constant’” is not really a constant – it is different at different cosmological times. The greater the value of the Hubble constant at a given cosmological time, the faster the universe is expanding at that time.
Dark energy
Although dark matter makes up most of the matter of the universe, it only makes up about a quarter of the composition of the universe. The universe is dominated by dark energy.

After the Big Bang, the universe began expanding outwards. Scientists once thought that it would eventually run out of the energy, slowing down as gravity pulled the objects inside it together (Big Crunch). But studies of distant supernovae revealed that the universe today is expanding faster than it was in the past, not slower, indicating that the expansion is accelerating (Big Rip). This would only be possible if the universe contained enough energy to overcome gravity – dark energy.
To understand the Big Crunch and the Big Rip as possible hypotheses of the end of the universe, see the link below.