
AP Precalculus FRQ: Detailed Solution
This problem involves analyzing and combining functions given in tabular and algebraic forms. Below is a step-by-step breakdown of each part of the question.
Given Information
1. The function f is decreasing and defined for all real numbers. Its values at selected points are given in the table:
| x | −2 | −1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| f(x) | 14 | 7 | 3.5 | 1.75 | 0.875 |
The function g is given by the equation: g(x) = −0.167x3 + x2 − 1.834.
Part A
This part deals with function composition and inverse functions.
i. Find the value of h(1).
The function h(x) is a composition of functions g and f, defined as h(x) = (g ˆ f)(x) = g(f(x)). To find h(1), we need to evaluate g(f(1)).
- Find the inner function value, f(1).
Look at the provided table. When the input x is 1, the output f(x) is 1.75.
So, f(1) = 1.75. - Use this result as the input for the outer function, g.
Now we need to calculate g(1.75). We substitute 1.75 for x in the equation for g(x):
g(1.75) = −0.167(1.75)3 + (1.75)2 − 1.834 - Calculate the final value.
g(1.75) = −0.167(5.359375) + (3.0625) − 1.834
g(1.75) = −0.894975625 + 3.0625 − 1.834
g(1.75) = 0.333524375
Approximated to three decimal places, h(1) ≈ 0.334.
ii. Find the value of f-1(3.5).
The expression f-1(y) asks for the input x that gives an output of y. So, finding f-1(3.5) means finding the value of x for which f(x) = 3.5.
- Look for the output value in the table.
Scan the f(x) row in the table to find the value 3.5. - Identify the corresponding input value.
The value 3.5 appears in the column where x = 0.
Therefore, because f(0) = 3.5, the inverse relationship is f-1(3.5) = 0. (Note: Since f is a decreasing function, it is one-to-one, which guarantees that its inverse f-1 exists.)
The value of f-1(3.5) is 0.
Part B
This part focuses on the properties of the polynomial function g(x).
i. Find all values of x for which g(x) = 0.
We need to find the roots (or zeros) of the function g(x). This means solving the cubic equation:
−0.167x3 + x2 − 1.834 = 0
Solving a cubic equation algebraically can be very complex. For AP Precalculus, this type of problem is typically solved using a graphing utility (like a graphing calculator).
- Graph the function y = g(x) on a graphing utility.
- Find the x-intercepts of the graph. The x-intercepts are the points where the graph crosses the x-axis, which corresponds to g(x) = 0.
Using a graphing calculator, we find three x-intercepts.
The values of x for which g(x) = 0 are approximately x ≈ −1.229, x ≈ 1.705, and x ≈ 5.513.
ii. Determine the end behavior of g as x increases without bound.
The end behavior of a polynomial function is determined by its leading term (the term with the highest power of x).
- Identify the leading term of g(x).
For g(x) = −0.167x3 + x2 − 1.834, the leading term is −0.167x3. - Analyze the leading term.
- The degree of the polynomial is 3 (an odd number).
- The leading coefficient is -0.167 (a negative number).
- Determine the end behavior.
For any polynomial with an odd degree and a negative leading coefficient, as the input x approaches positive infinity (x → ∞), the output g(x) will approach negative infinity (g(x) → −∞).
We express this using the mathematical notation of a limit.
The end behavior is: limx→∞ g(x) = −∞.
Part C
This part asks us to determine the type of function that best models the data for f(x).
i. Which function type best models function f: linear, quadratic, exponential, or logarithmic?
We test the data in the table to see which function model fits. The input values (x) increase by a constant interval of 1.
- Linear? A linear function has a constant rate of change (slope). The differences in outputs (Δf(x)) would be constant.
7 − 14 = −7
3.5 − 7 = −3.5
The differences are not constant, so it's not linear. - Exponential? An exponential function has a constant ratio of consecutive outputs for a constant change in inputs. Let's check the ratios.
f(−1) / f(−2) = 7 / 14 = 0.5
f(0) / f(−1) = 3.5 / 7 = 0.5
f(1) / f(0) = 1.75 / 3.5 = 0.5
f(2) / f(1) = 0.875 / 1.75 = 0.5
The ratio is constant (0.5). This is the signature of an exponential function.
The function type that best models f is exponential.
ii. Give a reason for your answer in part C (i).
The reasoning is based on the analysis performed above. We must explain how the changes in inputs and outputs lead to our conclusion.
Reasoning:
The function f is best modeled by an exponential function because for a constant additive change in the input values of x, there is a constant multiplicative change in the output values of f(x).
As shown in the table, the input x increases by a constant value of 1 at each step. When we calculate the ratio of consecutive output values, we get a constant factor:
f(x+1) / f(x) = 0.5 for all adjacent values in the table.
This constant ratio (or common ratio) is the defining characteristic of an exponential function.

AP Precalculus FRQ: Detailed Solution
This problem involves creating and analyzing a quadratic model for the total number of plays of a song.
Given Information
The total number of plays, D, in thousands, is modeled by the quadratic function D(t) = at2 + bt + c, where t is the number of months after an app was used to start counting.
The data from the table gives us three points:
- At t = 0, D(0) = 25
- At t = 2, D(2) = 30
- At t = 4, D(4) = 34
Part A
This part involves setting up and solving a system of equations to find the coefficients of the quadratic model.
i. Write three equations for the constants a, b, c.
We substitute each data point (t, D(t)) into the general quadratic equation D(t) = at2 + bt + c.
- For the point (0, 25):
D(0) = a(0)2 + b(0) + c = 25
This simplifies to: c = 25 - For the point (2, 30):
D(2) = a(2)2 + b(2) + c = 30
This simplifies to: 4a + 2b + c = 30 - For the point (4, 34):
D(4) = a(4)2 + b(4) + c = 34
This simplifies to: 16a + 4b + c = 34
The three equations are:
1. c = 25
2. 4a + 2b + c = 30
3. 16a + 4b + c = 34
ii. Find the values for a, b, c.
We now solve this system of linear equations.
- Use the value of c.
From the first equation, we already know c = 25. - Substitute c into the other two equations.
For equation 2: 4a + 2b + 25 = 30 ⇒ 4a + 2b = 5
For equation 3: 16a + 4b + 25 = 34 ⇒ 16a + 4b = 9 - Solve the new 2x2 system.
We have:
(Eq. A) 4a + 2b = 5
(Eq. B) 16a + 4b = 9
Multiply Eq. A by -2 to eliminate b: −2(4a + 2b) = −2(5) ⇒ −8a − 4b = −10.
Add this new equation to Eq. B:
(−8a − 4b) + (16a + 4b) = −10 + 9
8a = −1 ⇒ a = −1/8 = −0.125 - Find b.
Substitute a = −0.125 back into Eq. A:
4(−0.125) + 2b = 5
−0.5 + 2b = 5
2b = 5.5 ⇒ b = 2.75
The values for the constants are:
a = −0.125, b = 2.75, and c = 25.
The model is D(t) = −0.125t2 + 2.75t + 25.
Part B
This part focuses on the average rate of change and its interpretation.
i. Find the average rate of change of the total number of plays from t = 0 to t = 4 months.
The average rate of change is calculated using the formula: (D(t2) − D(t1)) / (t2 − t1).
Using the points from the table, (t1, D(t1)) = (0, 25) and (t2, D(t2)) = (4, 34).
Average Rate of Change = (D(4) − D(0)) / (4 − 0) = (34 − 25) / 4
= 9 / 4 = 2.25
The average rate of change is 2.25 thousand plays per month.
ii. Use the average rate of change to estimate the total plays for t = 1.5 months.
We can form a linear approximation, At, based on the starting point D(0) and the average rate of change. The formula is At = D(0) + (Average Rate) × t.
A1.5 = D(0) + (2.25) × 1.5
A1.5 = 25 + 3.375 = 28.375
The estimated total number of plays at t = 1.5 months is 28.375 thousand plays.
iii. Explain why At < D(t) for all t where 0 < t < 4.
First, we show that A1.5 < D(1.5). We calculated A1.5 = 28.375. Now we find the actual value D(1.5) using our model from Part A.
D(1.5) = −0.125(1.5)2 + 2.75(1.5) + 25
D(1.5) = −0.125(2.25) + 4.125 + 25
D(1.5) = −0.28125 + 4.125 + 25 = 28.84375
Indeed, 28.375 < 28.84375, so A1.5 < D(1.5).
General Explanation:
The linear estimation At represents the secant line connecting the points (0, D(0)) and (4, D(4)) on the graph of D(t).
The function D(t) = −0.125t2 + 2.75t + 25 is a quadratic with a negative leading coefficient (a = −0.125 < 0). This means the graph of D(t) is a parabola that opens downward, making it concave down everywhere.
For any concave down function, the graph of the function lies above its secant lines. Since At is the secant line on the interval from t=0 to t=4, the curve of D(t) must be above the line At for all values of t between 0 and 4. Therefore, At < D(t) for 0 < t < 4.
Part C
This part asks us to use the properties of the quadratic model to determine a reasonable domain based on the real-world context.
Explain how the maximum of the function D can be used to determine a boundary for the domain.
Real-World Context: The function D(t) represents the total number of plays since the song's release. A total, or cumulative, count cannot decrease over time. Therefore, for the model to be physically realistic, the function D(t) must be non-decreasing.
- Analyze the Model's Behavior: Our function D(t) = −0.125t2 + 2.75t + 25 is a downward-opening parabola, which means it increases to a maximum value and then decreases.
- Find the Maximum: The maximum of the parabola occurs at its vertex. The t-coordinate of the vertex is given by the formula t = −b / (2a).
tvertex = −(2.75) / (2 × −0.125)
tvertex = −2.75 / −0.25 = 11 - Interpret the Maximum: The vertex is at t = 11 months. This means the model predicts that the total number of plays increases for the first 11 months and then begins to decrease for t > 11.
- Apply the Restriction: Since the total number of plays cannot decrease, the model is only valid on the interval where it is non-decreasing. This corresponds to the part of the parabola from the start (t=0) up to its vertex.
The maximum of the function occurs at t = 11 months. After this time, the model predicts a decrease in total plays, which contradicts the real-world scenario. Therefore, the time of the maximum, t = 11, serves as a realistic upper boundary for the domain of the model D. A reasonable domain for this model would be 0 ≤ t ≤ 11.
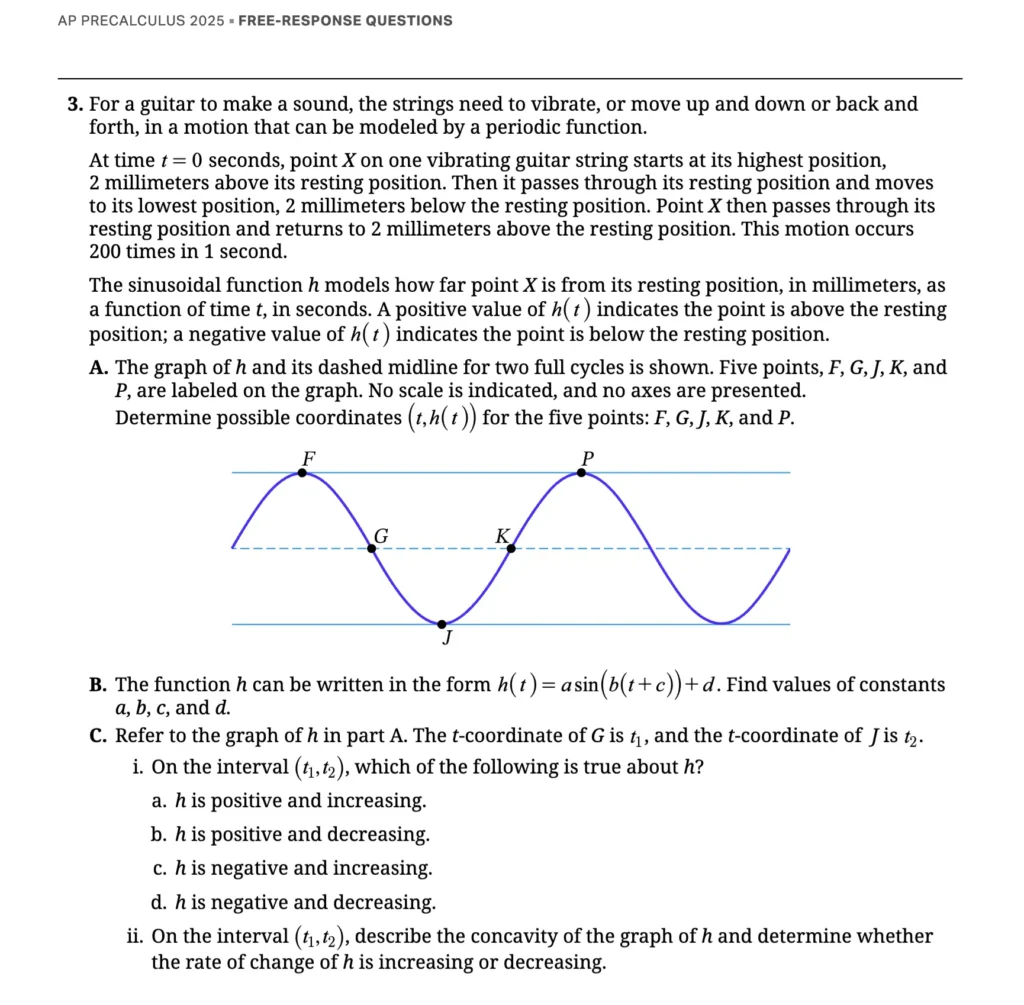
AP Precalculus FRQ: Detailed Solution
This problem models the vibration of a guitar string using a sinusoidal function. We'll break down how to find the key features of the function from the description and the graph.
Decoding the Problem
Before we start, let's extract the key parameters of the sinusoidal function h(t) from the text:
- Midline: The "resting position" corresponds to h(t) = 0. The midline of the graph is the horizontal line y = 0.
- Amplitude: The string moves between 2 mm *above* (+2) and 2 mm *below* (-2) the resting position. The amplitude is the distance from the midline to a maximum, which is 2.
- Frequency and Period: The motion occurs 200 times in 1 second. This is the frequency, f = 200 Hz. The period is the time for one full cycle, calculated as Period = 1 / frequency.
So, the period is T = 1/200 seconds. - Starting Point: At t = 0, the string is at its highest position. This means the graph starts at a maximum.
Part A: Determine Coordinates
We need to find the coordinates (t, h(t)) for the points F, G, J, K, and P using the parameters we just found.
One full cycle takes T = 1/200 seconds. The key points of a sinusoidal cycle occur at quarter-period intervals.
- Point F (Maximum): The problem states the graph starts at a maximum at t = 0. The maximum height is 2 mm.
Coordinates: F = (0, 2) - Point G (Midline, Decreasing): This occurs one-quarter of a period after the maximum.
t = 0 + T/4 = (1/200) / 4 = 1/800. The point is on the midline, so h(t) = 0.
Coordinates: G = (1/800, 0) - Point J (Minimum): This occurs one-half of a period after the maximum.
t = 0 + T/2 = (1/200) / 2 = 1/400. The minimum height is -2 mm.
Coordinates: J = (1/400, −2) - Point K (Midline, Increasing): This occurs three-quarters of a period after the maximum.
t = 0 + 3T/4 = 3 * (1/200) / 4 = 3/800. The point is on the midline.
Coordinates: K = (3/800, 0) - Point P (Next Maximum): This occurs one full period after the first maximum.
t = 0 + T = 1/200. The height is again at the maximum.
Coordinates: P = (1/200, 2)
- F = (0, 2)
- G = (1/800, 0)
- J = (1/400, −2)
- K = (3/800, 0)
- P = (1/200, 2)
Part B: Find the Equation
We need to find the values of the constants a, b, c, and d for the function h(t) = a sin(b(t + c)) + d.
- Constant d (Vertical Shift): The vertical shift is the value of the midline. The midline is the resting position, y = 0. Therefore, d = 0.
- Constant a (Amplitude): The amplitude is the distance from the midline to a maximum. The maximum is 2. So, a = 2.
- Constant b (Frequency Multiplier): This constant is related to the period T by the formula T = 2π/|b|. We know T = 1/200.
1/200 = 2π/b ⇒ b = 2π × 200 = 400π. - Constant c (Phase Shift): The phase shift determines the horizontal starting position. A standard sine function, y = sin(x), starts at the midline and increases. Our graph starts at a maximum. We need to shift the sine function to match.
A sine function reaches its first maximum at x = π/2. We want the argument of our sine function to be π/2 when t = 0.
The argument is b(t + c). So we set:
b(0 + c) = π/2
(400π)c = π/2
c = (π/2) / (400π) = 1/800.
The values of the constants are:
a = 2, b = 400π, c = 1/800, d = 0.
The function is h(t) = 2 sin(400π(t + 1/800)).
Alternative approach: It's often easier to model a function starting at a maximum with a cosine function: h(t) = 2 cos(400πt). Using the identity cos(x) = sin(x + π/2), we get h(t) = 2 sin(400πt + π/2). Factoring out 400π gives h(t) = 2 sin(400π(t + 1/800)), confirming our value for c.
Part C: Analyze Graph Behavior
This part asks about the properties of h(t) on the interval from t1 (the t-coordinate of G) to t2 (the t-coordinate of J).
From Part A, we know t1 = 1/800 and t2 = 1/400. We are analyzing the behavior of the graph on the interval (1/800, 1/400), which is the segment from point G to point J.
i. On the interval (t1, t2), which statement is true?
- Sign of h: On the interval from G to J, the entire curve is below the t-axis (the midline). This means the function's values are negative. So, h is negative.
- Direction of h: As we move from left to right (from G to J), the graph is moving downward. This means the function is decreasing.
Combining these observations, h is negative and decreasing on the interval. This corresponds to option (d).
ii. Describe the concavity and the rate of change on (t1, t2).
We are still looking at the segment of the graph between points G and J.
- Concavity: The shape of the curve between G and J is "cupped up," like the bottom of a bowl. This shape is defined as concave up.
- Rate of Change: The rate of change is the slope of the function.
- At point G, the slope is negative.
- At point J (a minimum), the slope is zero.
A key concept is that if a function is concave up on an interval, its rate of change (or derivative) is increasing on that interval.
On the interval (t1, t2), the graph of h is concave up, and the rate of change of h is increasing.

AP Precalculus FRQ: Detailed Solution
This problem tests your ability to solve various types of equations and simplify expressions involving logarithmic, trigonometric, and exponential functions.
Part A: Solving Equations
i. Solve g(x) = 4 for g(x) = 2 log3x.
We need to solve the equation 2 log3x = 4.
- Isolate the logarithm. Divide both sides by 2:
log3x = 2 - Convert to exponential form. The equation logba = c is equivalent to bc = a. Applying this rule:
x = 32 - Calculate the final value.
x = 9 - Check the domain. The domain of log3x is x > 0. Our solution x = 9 is in the domain.
The solution is x = 9.
ii. Solve h(x) = 3 for h(x) = 4 cos2x in the interval [0, π/2].
We need to solve the equation 4 cos2x = 3.
- Isolate the trigonometric term. Divide both sides by 4:
cos2x = 3/4 - Take the square root. Remember to include both positive and negative roots:
cos x = ±√(3/4) = ±√3 / 2 - Consider the given interval. The interval is [0, π/2], which is Quadrant I. In Quadrant I, the value of cosine is always positive.
- Solve for x. We only need to solve cos x = +√3 / 2. From our knowledge of the unit circle, the angle in Quadrant I that satisfies this equation is:
x = π/6
The solution in the interval [0, π/2] is x = π/6.
Part B: Rewriting Functions
i. Rewrite j(x) = log2x + 3 log22 as a single logarithm.
We need to combine the terms into the form log2(expression) using logarithm properties.
- Apply the Power Rule. The power rule, n logba = logb(an), can be applied to the second term:
3 log22 = log2(23) = log28 - Substitute back into the expression. The function is now:
j(x) = log2x + log28 - Apply the Product Rule. The product rule, logba + logbc = logb(ac), allows us to combine the two terms:
j(x) = log2(x · 8)
The function as a single logarithm is j(x) = log2(8x).
ii. Rewrite k(x) = 6 / (tan x(csc2x − 1)) so tan x appears once.
We need to simplify the expression using trigonometric identities.
- Simplify the denominator. Look at the term (csc2x − 1). Recall the Pythagorean identity: 1 + cot2x = csc2x.
- Rearrange the identity. Subtracting 1 from both sides gives cot2x = csc2x − 1.
- Substitute into the denominator.
tan x(csc2x − 1) = tan x(cot2x) - Use the Reciprocal Identity. We know that cot x = 1 / tan x. Therefore, cot2x = 1 / tan2x.
tan x(cot2x) = tan x · (1 / tan2x) = tan x / tan2x = 1 / tan x - Substitute the simplified denominator back into k(x).
k(x) = 6 / (1 / tan x) - Simplify the complex fraction. Dividing by a fraction is the same as multiplying by its reciprocal.
k(x) = 6 · tan x
The simplified expression is k(x) = 6 tan x.
Part C: Solving an Exponential Equation
Find all input values for m(x) = e2x − ex − 12 that yield an output of 0.
We need to solve the equation m(x) = 0, which is e2x − ex − 12 = 0.
- Recognize the quadratic form. Notice that e2x = (ex)2. The equation can be rewritten as:
(ex)2 − (ex) − 12 = 0 - Use substitution. To make it look like a standard quadratic, let u = ex. The equation becomes:
u2 − u − 12 = 0 - Factor the quadratic. We need two numbers that multiply to -12 and add to -1. These numbers are -4 and 3.
(u − 4)(u + 3) = 0 - Solve for u. This gives two possible solutions for u:
u = 4 or u = −3 - Substitute back and solve for x.
- Case 1: u = 4
Substitute back ex for u: ex = 4.
To solve for x, take the natural logarithm of both sides:
ln(ex) = ln(4) ⇒ x = ln(4). - Case 2: u = −3
Substitute back ex for u: ex = −3.
The function ex is always positive for any real number x. Therefore, there is no real solution for this case.
- Case 1: u = 4
The only input value that yields an output of 0 is x = ln(4).

