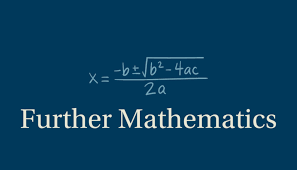Solving Quadratics – GCSE Algebra Guide
“If algebra is a puzzle, then quadratics are the corner pieces. Once you master them, everything starts to make sense.”
🎯 Introduction: Why Quadratics Matter More Than You Think
We get it — the word “quadratic” sounds like something out of a sci-fi film. But here’s the thing: quadratic equations show up everywhere. Whether you’re calculating projectile motion in physics or optimizing profits in business, mastering them unlocks the real magic of algebra.
So, whether you’re a GCSE student staring at your textbook like it’s written in an alien language, a parent trying to help, or a tutor looking to make things click — this guide’s for you.
We’ll walk you through the core techniques, real-world examples, and examiner-approved strategies to help you confidently solve any quadratic thrown your way.
Let’s dive in.
🔍 What Is a Quadratic Equation?
A quadratic equation is any equation that can be written in the form:
ax² + bx + c = 0
Where:
a,b, andcare numbers (anda ≠ 0),xis the unknown variable,and the highest exponent is 2.
Examples:
x² - 5x + 6 = 02x² + 3x - 2 = 0
🧠 Methods for Solving Quadratics (GCSE Focus)
There are four main methods taught in the GCSE curriculum. Each one has its moment.
1. Factorising
Used when the equation can be broken into two brackets:
x² - 5x + 6 = 0 → (x - 2)(x - 3) = 0
From here, we set each bracket to zero:
x - 2 = 0 → x = 2
x - 3 = 0 → x = 3
✅ Fastest method if it works. Great for mental maths and non-calculator papers.
2. Using the Quadratic Formula
When factorising isn’t working, use this:
x = (-b ± √(b² - 4ac)) / 2a
📌 Example:
2x² + 3x - 2 = 0
a = 2, b = 3, c = -2
Plug into formula:
x = (-3 ± √(3² - 4×2×-2)) / 2×2
= (-3 ± √(9 + 16)) / 4
= (-3 ± √25) / 4
So, x = (2)/4 = 0.5 or x = (-8)/4 = -2
✅ Always works, especially for tough coefficients.
3. Completing the Square
This technique rewrites the quadratic in a perfect square form.
📌 Useful for:
Understanding graph shapes
Finding turning points
Some exam questions requiring exact forms
Example:
x² + 6x + 10
→ (x + 3)² + 1
4. Solving by Graphing
Plot the quadratic equation using a graphing calculator or app like Desmos or GeoGebra.
The points where the graph crosses the x-axis = your solutions
If it doesn’t cross, there are no real roots
✅ Excellent for visual learners and real-life applications
🎯 When to Use Which Method?
| Method | Best When… |
|---|---|
| Factorising | Equation is easy to split into brackets |
| Quadratic Formula | Factorising is tricky or involves decimals/fractions |
| Completing the Square | Exact answers or turning points needed |
| Graphing | You need to visualise or estimate solutions |
💡 Real-World Uses of Quadratics
Physics: Trajectories, velocity-time problems
Business: Maximizing revenue or minimizing cost
Engineering: Structural design, parabolas
Computer Graphics: Modelling curves and motion
“Solving x² + 6x + 9 = 0 might seem pointless… until you realise it’s how your GPS calculates curves in your driving route.”
🧪 Common Mistakes (And How to Avoid Them)
❌ Forgetting to set the equation to 0 before solving
❌ Incorrect signs when factorising or applying the formula
❌ Misreading b² as b × 2 in the formula (watch for this!)
❌ Not checking your answers by substitution
✅ Always double-check by plugging your solutions back into the original equation.
🧘♂️ Mindset Matters: From Frustrated to Fluent
“I used to dread quadratics. But once I understood the logic behind each method, it felt like solving puzzles — and I started to actually enjoy them.” – Amaan, Year 11 GCSE Student, London
If you’ve been intimidated by algebra, know this: quadratics are beatable. Not with brute memorization, but with pattern recognition, method practice, and real understanding.
Start small. Try one problem per day. Use colours, diagrams, even songs. Make math your own.
📚 More Resources on HeLovesMath.com
GCSE Algebra: Mastering Factorisation
GCSE Graphs & Functions: Interactive Practice
Quadratic Equation Calculator Tool
🏁 Conclusion: Your Algebra Superpower Awaits
Solving quadratics isn’t just about passing your GCSEs — it’s about unlocking your confidence in math. Because when you can handle a tricky equation and come out with x = 3 or x = -2, you’re training your brain to solve bigger life problems, too.
So keep going. You’re closer than you think.
“Math isn’t about numbers. It’s about clarity, curiosity, and courage.”
❓ People Also Ask (FAQs):
Q1. What are the 4 ways to solve a quadratic equation?
A: Factorising, using the quadratic formula, completing the square, and graphing.
Q2. What is the easiest way to solve quadratics for GCSE?
A: Factorising is the quickest method if it works, but the quadratic formula always works and is reliable for tricky cases.
Q3. How do I know which method to use?
A: It depends on the question format. If the quadratic factors easily, use factorising. If not, go for the formula or completing the square.
Q4. Why are quadratics important?
A: They’re used in physics, engineering, business, and tech. Mastering them builds algebra skills that apply far beyond exams.
Keep solving. Keep learning. You’ve got this! 💪